题目内容
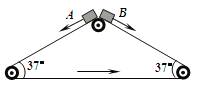
【题目】如图所示，水平传送带的左端与一倾角θ=37°的粗糙斜面平滑连接，一个小滑块（可视为质点）从斜面上的A点由静止释放，沿斜面滑下并冲上传送带，传送带以恒定速率v=2m/s逆时针转动．已知小滑块的质量m=2kg，斜面上A点到斜面底端的长度s=9m，传送带的长度为L=10m，小滑块与斜面的动摩擦因数μ1=0.50，小滑块与传送带间动摩擦因数μ2=0.40，g=10m/s2．求：
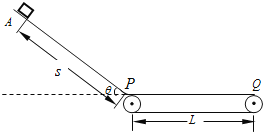
（1）小滑块到达斜面底端P的速度大小；
（2）a．判断冲上传送带的小滑块是否可以运动到传送带的右端Q；
b．若小滑块可以运动到Q，试求小滑块从P点运动到Q点的过程中摩擦力分别对小滑块和传送带做的功；若小滑块不能达到Q，试求小滑块从P点开始再次运动到P点过程中摩擦力分别对小滑块和传送带做的功；
（3）小滑块在斜面和传送带上运动的整个过程中，小滑块相对于地面的总路程．
【答案】（1）6m/s；（2）a．不能到Q；b．-32J；-32J；（3）13.5m
【解析】（1）滑块下滑过程，由动能定理得：
mgssinθ﹣μ1mgcosθs=
mvP2﹣0，
代入数据解得：vP=6m/s；
（2）a、滑块到达传送带上后做匀减速直线运动，在滑块速度减为零过程中，由动能定理得：
﹣μ2mgs′=0﹣
mvP2，
代入数据解得：s′=4.5m＜L=10m，滑块不能到达Q端；
b、滑块在传送带上运动时的加速度为：a=
=μ2g=4m/s2，
滑块向右减速运动的时间为： 
，
在此时间内，传送带位移为：x1=vt1=2×1.5=3m，
滑块向右加速运动到速度等于传送带速度需要的时间为： 
，
在此时间内传送带的位移为：x2=vt2=2×0.5=1m，
在整个过程中，摩擦力对传送带做功为：W传送带=﹣μ2mg（x1+x2）=﹣32J，
由动能定理可知，整个过程摩擦力对滑块做功为：W滑块=
mv2﹣
mvP2=﹣32J；
（3）滑块在运动过程中要考查摩擦力做功，使其机械能减少，最终滑块将静止在P处，有：
μ1cosθ=μ2=μ=0.4，
设滑块在整个过程中相对水平地面的路程为s总，对滑块由动能定理得：mgssinθ=μmgs总，
代入数据解得：s总=13.5m；
点睛; 本题考查了动能定理的应用，分析清楚滑块的运动过程是解题的关键，应用动能定理可以解题．分析滑块运动过程时要注意：滑块在传送带上向左先做匀加速运动，后做匀速直线运动；解题时要注意，（3）求的是滑块相对地面的路程．
