��Ŀ����
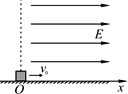
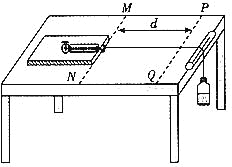
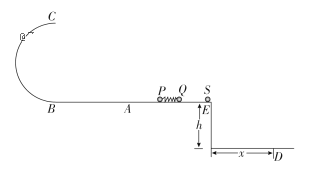
����Ŀ����ͼ��ʾ���ڹ⻬ˮƽ����EAB��������Ϊm��2 kg��С��P������ΪM��1 kg��С��Q��P��Q֮��ѹ��һ�ᵯ��(�ᵯ������С��˩��)�������ԵE������һ����ҲΪM��1 kg����Ƥ����S����B���̶�һ��ˮƽ�������еĹ⻬��ֱ��Բ�ι�����ͷű�ѹ�����ᵯ�ɣ�P��Q��С���ᵯ�ɵ�����С��P�뵯�ɷ��������Բ�ι����ǡ���ܹ�ͨ����Բ�ι������ߵ�C��С��Q�뵯�ɷ�����������Ե����Ƥ����S��ײ���Ϊһ��ɳ�������ˮƽ�����ϵ�D�㡣��֪ˮƽ�����Ϊh��0.2 m��D�㵽�����Ե��ˮƽ����Ϊx��0.2 m���������ٶ�Ϊg��10 m/s2����
(1)С��P������Բ�ι����͵�Bʱ�Թ����ѹ����СNB����
(2)С��Q����Ƥ����S��ײǰ˲����ٶȴ�СvQ��
(3)��ѹ�����ᵯ�ɵĵ�������Ep��
���𰸡�(1)120N��(2)2 m/s��(3)3 J
��������
��1��С��Pǡ����ͨ����Բ�ι������ߵ�C������
mg��m![]()
���
vC��![]()
����С��P����B��C���ɶ��ܶ�����
![]()
���
vB��![]()
��B����
NB��mg��m![]()
���
NB��6mg��120 N
��ţ�ٵ���������
NB����NB��120 N
��2����Q��S��ƽ���˶��ij��ٶȴ�СΪv������ʱ��Ϊt�����ݹ�ʽh��![]() gt2����
gt2����
t��0.2 s
���ݹ�ʽx��vt����
v��1 m/s
��ײǰ��Q��S��ɵ�ϵͳ�����غ㣬
����
MvQ��2Mv
���
vQ��2 m/s
��3��P��Q�͵�����ɵ�ϵͳ�����غ㣬
����
mvP��MvQ
���
vP��1 m/s
��P��Q�͵�����ɵ�ϵͳ���������غ㶨����
![]()
���
Ep��3 J

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�