题目内容
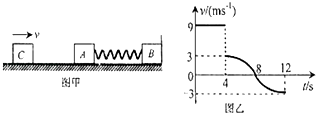
【题目】如图甲所示，物块A、B间拴接一个压缩后被锁定的弹簧，整个系统静止放在光滑水平地面上，其中A物块最初与左侧固定的挡板相接触，B物块质量为2kg．现解除对弹簧的锁定，在A离开挡板后，B物块的v﹣t图如图乙所示，则可知（ ）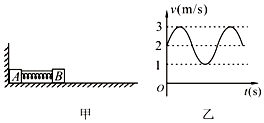
A.A的质量为4kg
B.运动过程中A的最大速度为vm=4m/s
C.在A离开挡板前，系统动量守恒、机械能守恒
D.在A离开挡板后弹簧的最大弹性势能为3J
【答案】B,D
【解析】解：A、弹簧伸长最长时弹力最大，B的加速度最大，此时AB共速，由图知，AB共同速度为 v共=2m/s，A刚墙时B的速度为 v0=3m/s．
在A离开挡板后，取向右为正方向，由动量守恒定律，有：mBv0=（mA+vB）v共
解得 mA=1kg，故A错误．
B、当弹簧第一次恢复原长时A的速度最大，由mBv0=mAvA+mBvB
mBv02= mAvA2+ mBvB2．
解得：A的最大速度 vA=4m/s，故B正确．
C、在A离开挡板前，由于挡板对A有作用力，A、B系统所受合外力不为零，所以系统动量不守恒；故C错误．
D、分析A离开挡板后A、B的运动过程，并结合图象数据可知，弹簧伸长到最长时A、B的共同速度为v共=2m/s，
根据机械能守恒定律和动量守恒定律，有：mBv0=（mA+mB）v共
Ep= mBv02﹣ （mA+mB）v共2．
联立解得：弹簧的最大弹性势能 Ep=3J，故D正确．
故选：BD
【考点精析】解答此题的关键在于理解弹性势能的相关知识，掌握弹性势能是物体由于发生弹性形变而具有的能量，以及对功能关系的理解，了解当只有重力（或弹簧弹力）做功时，物体的机械能守恒；重力对物体做的功等于物体重力势能的减少:W G =E p1 -E p2；合外力对物体所做的功等于物体动能的变化:W 合 =E k2 -E k1 （动能定理）；除了重力（或弹簧弹力）之外的力对物体所做的功等于物体机械能的变化:W F =E 2 -E 1．
