题目内容
【题目】如图所示，在第一象限有一匀强电场，场强大小为E，方向与y轴平行；一质量为m、电荷量为－q(q>0)的粒子以平行于x轴的速度从y轴上P点处射入电场，已知OP＝L，OQ＝2
L.不计粒子重力．求：
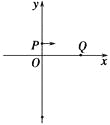
(1)粒子在第一象限中运动的时间．
(2)粒子离开第一象限时速度方向与x轴的夹角．
【答案】（1）
（2）
【解析】
本题考查了带电粒子在电场中的偏转问题，在电场方向做匀变速直线运动，在初速度方向做匀速直线运动，据此分析
(1)带电粒子在电场中做类平抛运动，在y轴负方向上做初速度为零的匀加速运
动，设加速度的大小为a，在x轴正方向上做匀速直线运动，设速度为v0，粒子从P点
运动到Q点所用的时间为t，则由类平抛运动的规律可得：
①
2
l＝v0t ②
且
③
由①③式得：
. ④
(2)设粒子射出第一象限时速度方向与x轴正方向的夹角为θ则
⑤
由②③④⑤式，得tan θ＝
，即θ＝30°.
思路拓展：做此类问题的关键是弄明白粒子在各个方向上的运动情况，然后根据受力分析结合牛顿运动定律分析解题，
练习册系列答案
相关题目
