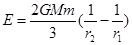题目内容
物体在万有引力场中具有的势能叫做引力势能。取两物体相距无穷远时的引力势能为零,一个质量为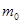 的质点距离质量为M0的引力源中心为
的质点距离质量为M0的引力源中心为 时。其引力势能
时。其引力势能 (式中G为引力常数)。现有一颗质量为
(式中G为引力常数)。现有一颗质量为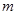 的人造地球卫星以圆形轨道环绕地球飞行,由于受高空稀薄空气的阻力作用,卫星的圆轨道半径从
的人造地球卫星以圆形轨道环绕地球飞行,由于受高空稀薄空气的阻力作用,卫星的圆轨道半径从 缓慢减小到
缓慢减小到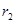 。已知地球的半径为R,地球表面的重力加速度为g,求此过程中卫星克服空气阻力做功。(用m、R、g、
。已知地球的半径为R,地球表面的重力加速度为g,求此过程中卫星克服空气阻力做功。(用m、R、g、 、
、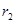 表示)
表示)
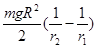
解析试题分析:设卫星轨道半径为r时,
由: 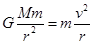 ① (M为地球的质量) (2分)
① (M为地球的质量) (2分)
由题目条件 其引力势能为: 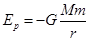 ② (1分)
② (1分)
由①②得:
卫星在在r处时的总能量(动能与引力势能之和)为:  ③ ( 1分)
③ ( 1分)
故半径为r1时,卫星总能量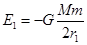 ④ (1分)
④ (1分)
故半径为r2时,其总能量 ⑤ (1分)
⑤ (1分)
由功能关系关系得:卫星轨道变化过程中克服阻力的功 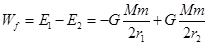 ⑥ (3分)
⑥ (3分)
又由: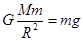 ⑦ (2分)
⑦ (2分)
由⑥⑦得: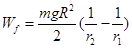 (1分)
(1分)
考点:万有引力定律的应用
点评:中等难度。引力势能实际是重力势能的另一种表现形式,克服阻力做的功等于卫星损失的机械能(动能与引力势能之和),千万注意不要丢了动能。

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
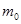 的质点距离质量为M0的引力源中心为
的质点距离质量为M0的引力源中心为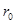 时。其引力势能
时。其引力势能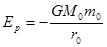 (式中G为引力常数)。现有一颗质量为
(式中G为引力常数)。现有一颗质量为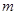 的人造地球卫星以圆形轨道环绕地球飞行,由于受高空稀薄空气的阻力作用,卫星的圆轨道半径从
的人造地球卫星以圆形轨道环绕地球飞行,由于受高空稀薄空气的阻力作用,卫星的圆轨道半径从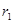 缓慢减小到
缓慢减小到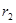 。已知地球的半径为R,地球表面的重力加速度为g,求此过程中卫星克服空气阻力做功。(用m、R、g、
。已知地球的半径为R,地球表面的重力加速度为g,求此过程中卫星克服空气阻力做功。(用m、R、g、 (式中G为引力常数)。一颗质量为m的人造地球卫星以半径为r1圆形轨道环绕地球飞行,已知地球的质量为M,要使此卫星绕地球做匀速圆周运动的轨道半径增大为r2,则卫星上的发动机所消耗的最小能量为( )
(式中G为引力常数)。一颗质量为m的人造地球卫星以半径为r1圆形轨道环绕地球飞行,已知地球的质量为M,要使此卫星绕地球做匀速圆周运动的轨道半径增大为r2,则卫星上的发动机所消耗的最小能量为( ) B.
B.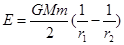
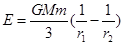 D.
D.