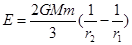题目内容
物体在万有引力场中具有的势能叫做引力势能.取两物体相距无穷远时的引力势能为零,一个质量为m0的质点距离质量为M0的引力源中心为r0时.其引力势能Ep=-
(式中G为引力常数),一颗质量为m的人造地球卫星以圆形轨道环绕地球飞行,已知地球的质量为M,由于受高空稀薄空气的阻力作用.卫星的圆轨道半径从r1逐渐减小到r2.若在这个过程中空气阻力做功为Wf,则在下面给出的Wf的四个表达式中正确的是( )
| GM0m0 |
| r0 |
分析:求出卫星在半径为r1圆形轨道和半径为r2的圆形轨道上的动能,从而得知动能的减小量,通过引力势能公式求出势能的增加量,根据能量守恒求出发动机所消耗的最小能量.
解答:解:卫星在圆轨道半径从r1上时,根据万有引力提供向心力:
=
解得Ek1=
m
=
.
卫星的总机械能:E1=Ek1+EP1=
-
=-
同理:卫星的圆轨道半径从r2上时,Ek2=
卫星的总机械能:E2=-
卫星的圆轨道半径从r1逐渐减小到r2.在这个过程中空气阻力做功为Wf,等于卫星机械能的减少:Wf=△E=E2-E1=-
(
-
).所以选项B正确.
故选:B.
| GMm | ||
|
m
| ||
| r1 |
解得Ek1=
| 1 |
| 2 |
| v | 2 1 |
| GMm |
| 2r1 |
卫星的总机械能:E1=Ek1+EP1=
| GMm |
| 2r1 |
| GMm |
| r1 |
| GMm |
| 2r1 |
同理:卫星的圆轨道半径从r2上时,Ek2=
| GMm |
| 2r2 |
卫星的总机械能:E2=-
| GMm |
| 2r2 |
卫星的圆轨道半径从r1逐渐减小到r2.在这个过程中空气阻力做功为Wf,等于卫星机械能的减少:Wf=△E=E2-E1=-
| GMm |
| 2 |
| 1 |
| r2 |
| 1 |
| r1 |
故选:B.
点评:解决本题的关键得出卫星动能和势能的和即机械能的变化量,从而根据能量守恒进行求解.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
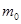 的质点距离质量为M0的引力源中心为
的质点距离质量为M0的引力源中心为 时。其引力势能
时。其引力势能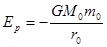 (式中G为引力常数)。现有一颗质量为
(式中G为引力常数)。现有一颗质量为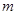 的人造地球卫星以圆形轨道环绕地球飞行,由于受高空稀薄空气的阻力作用,卫星的圆轨道半径从
的人造地球卫星以圆形轨道环绕地球飞行,由于受高空稀薄空气的阻力作用,卫星的圆轨道半径从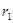 缓慢减小到
缓慢减小到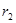 。已知地球的半径为R,地球表面的重力加速度为g,求此过程中卫星克服空气阻力做功。(用m、R、g、
。已知地球的半径为R,地球表面的重力加速度为g,求此过程中卫星克服空气阻力做功。(用m、R、g、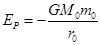 (式中G为引力常数)。一颗质量为m的人造地球卫星以半径为r1圆形轨道环绕地球飞行,已知地球的质量为M,要使此卫星绕地球做匀速圆周运动的轨道半径增大为r2,则卫星上的发动机所消耗的最小能量为( )
(式中G为引力常数)。一颗质量为m的人造地球卫星以半径为r1圆形轨道环绕地球飞行,已知地球的质量为M,要使此卫星绕地球做匀速圆周运动的轨道半径增大为r2,则卫星上的发动机所消耗的最小能量为( )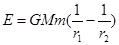 B.
B.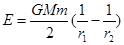
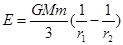 D.
D.