题目内容
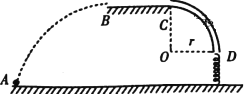
【题目】如图甲所示,电荷量均为+q、质量分别为m1和m2的两个离子飘入电压为U0的加速电场,其初速度几乎为零。离子经加速后通过狭缝O沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场,质量为m1的离子最后打在底片MN的中点P上。已知放置底片的区域MN=L,底片能绕着轴M顺时针转动,OM=L。不计离子间的相互作用。sin![]() =0.6,sin
=0.6,sin![]() =0.8,tan
=0.8,tan![]() =
=![]()
(1)求打在MN中点P的离子质量m1;
(2)已知m1=4m2,质量为m2的离子无法打到底片上,但可以绕轴M转动底片,使离子的运动轨迹与底片相切,求运动轨迹与底片相切时底片转过的角度;
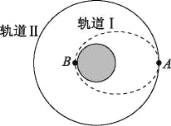
(3)若将偏转磁场改为半径R=![]() L,圆心在O1处的圆形磁场,磁感应强度大小仍为B,磁场方向垂直于纸面向里,磁场边界与直线MN相切于O点,如图乙所示。两个离子能否打到底片上?若能,求离子离开磁场后运动到底片的时间?
L,圆心在O1处的圆形磁场,磁感应强度大小仍为B,磁场方向垂直于纸面向里,磁场边界与直线MN相切于O点,如图乙所示。两个离子能否打到底片上?若能,求离子离开磁场后运动到底片的时间?

【答案】(1)![]() (2)
(2)![]() (3)m1不能,m2能,
(3)m1不能,m2能,![]()
【解析】
(1)离子在电场中加速
qU0=![]() m1v12
m1v12
在磁场中做匀速圆周运动
qv1B=m1![]()
解得
r1=![]()
代入r1=![]() L解得
L解得
![]()
(2)由(1)可知
![]()
如图1
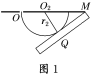
Q为轨迹与底片的切点
|O2M|=L-r2=![]() L
L
sin∠O2MQ=![]() =0.6
=0.6
所以∠O2MQ=![]() ,所以,运动轨迹与底片相切时底片转过
,所以,运动轨迹与底片相切时底片转过![]() ,
,
(3)质量为m1的离子离开磁场后速度方向与底片平行,不能打到底片上,质量为m2的离子能打在底片上。根据第(2)问,过O点做OM的垂线与底片延长线交于A点,如图2
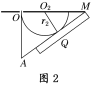
|OA|=Ltan![]() =
=![]() L=R
L=R
故A点即为磁场的圆心O1,所以质量为m2的离子打在底片上的M点。
质量为m2的离子从A点离开磁场后做匀速直线运动,与底片交于B点,连接O1O2、O2A、O1B,如图3
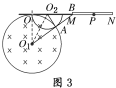
tan∠OO1O2=![]() =0.5
=0.5
tan∠OO1O2=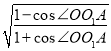
cos∠OO1A=0.6
∠OO1A=![]()
∠O2BA=![]()
B与M重合,质量为m2的离子打在底片上的M点,离子离开磁场后做匀速直线运动
|AM|=![]() -R=
-R=![]() L
L
由
qU0=![]() m2v22
m2v22
得
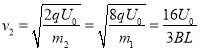
离子离开磁场后的运动时间为
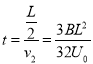

 名校课堂系列答案
名校课堂系列答案