题目内容
【题目】如图所示，一个光滑斜面与一个光滑的竖直圆轨道在A点相切，B点为圆轨道的最低点，C点为圆轨道的最高点，整个空间存在水平向左的匀强电场。一质量为m=1kg，电荷量为+q的带电小球从斜面上距A点s=2m处的O点静止释放．已知电场强度
，θ=53°，圆轨道半径R=1m，(g取10m/s2，sin53°=0.8，cos53°=0.6)。求：(结果保留两位有效数字)
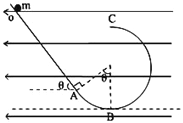
(1)小球经过B点时受到的支持力的大小；
(2)为了使小球能经过C点，小球应在斜面上至少离A点多远处静止释放?
【答案】（1）20N （2）8.8m
【解析】（1）从O到B过程，由动能定理得：
mg[ssinθ+R（1﹣cosθ）]﹣qE（scosθ+Rsinθ）=
mvB2﹣0，
在B点，由牛顿第二定律得：N﹣mg=m
，解得：N=20N；
（2）小球恰好经过等效最高点，由牛顿第二定律得：5mg/4=m
，解得：v2=25/2，
小球从静止到该点过程，由动能定理得：
mg[Lsinθ﹣Rcosθ﹣Rsinθ）﹣2R]﹣qE（Lcosθ+Rsinθ+Rcosθ）=
mv2﹣0，
解得：L=8.8m；
练习册系列答案
相关题目
