题目内容
20. 倾角为37°的足够长光滑斜面上固定一个槽,劲度系数k=20N/m的轻弹簧上端与轻杆相连,下端与一质量m=1kg的小车相连,开始时,弹簧处于原长,轻杆在槽外的长度为l,且杆可在槽内移动,杆与槽间的最大静摩擦力大小f=8N,假设杆与槽之间的最大静摩擦力等于滑动摩擦力.现将小车由静止释放沿斜面向下运动,在小车第一次运动到最低点的过程中(已知弹性势能Ep=$\frac{1}{2}$kx2,式中x为弹簧的形变量.g=10m/s2,sin37°=0.6,cos37°=0.8)
倾角为37°的足够长光滑斜面上固定一个槽,劲度系数k=20N/m的轻弹簧上端与轻杆相连,下端与一质量m=1kg的小车相连,开始时,弹簧处于原长,轻杆在槽外的长度为l,且杆可在槽内移动,杆与槽间的最大静摩擦力大小f=8N,假设杆与槽之间的最大静摩擦力等于滑动摩擦力.现将小车由静止释放沿斜面向下运动,在小车第一次运动到最低点的过程中(已知弹性势能Ep=$\frac{1}{2}$kx2,式中x为弹簧的形变量.g=10m/s2,sin37°=0.6,cos37°=0.8)(1)当轻杆开始运动时,小车的速度有多大;
(2)为了使轻杆不被全部拽入槽内,求l的最小长度及在此长度下轻杆在槽内的运动时间.
分析 (1)轻杆开始运动时,弹簧对其拉力等于杆受到的最大静摩擦力;根据胡克定律列式求解弹簧的伸长量;根据功能关系列式求解小车的速度;
(2)杆被拉动后,根据牛顿第二定律列式求解加速度;此后小车和杆一起是匀减速直线运动,直到速度为零后被反向拉回;
解答 解:(1)轻杆开始运动时,弹簧对其拉力等于杆受到的最大静摩擦力,为:
F=f=8N;
根据胡克定律,有:
x=$\frac{F}{k}$=$\frac{8}{20}$=0.4m;
根据功能关系,有:
mgxsinθ-$\frac{1}{2}k{x}^{2}=\frac{1}{2}m{v}^{2}$
解得:
v=0.4$\sqrt{10}$m/s
(2)杆刚滑动时,对整体由牛顿第二定律得物体的加速度:
mgsin37°-F=ma
解得:
a=-2m/s2
此后小车和杆一起是匀减速直线运动,直到速度为零后被反向拉回;
根据速度位移公式,减速位移为:
x1=$\frac{{0}^{2}-{v}^{2}}{2a}$=$\frac{0-(0.4\sqrt{10})^{2}}{2×(-2)}$=0.4m
故杆的长度至少为0.4m;
对物块分析得,平衡位置对应的弹簧伸长量为:$△x=\frac{mgsin37°}{k}$=$\frac{1×10×0.6}{20}=0.3m$;
故反向弹回后,球开始在平衡位置附近做简谐运动,振幅为0.1m,杆不再移动;
故杆滑动的时间:t=$\frac{0-v}{a}$=$\frac{0-0.4\sqrt{10}}{-2}=0.2\sqrt{10}$s,
答:(1)当轻杆开始运动时,小车的速度为0.4$\sqrt{10}$m/s;
(2)l的最小长度为0.4m,在此长度下轻杆在槽内的运动时间为0.2$\sqrt{10}s$.
点评 本题关键是明确小车和杆的受力情况和运动情况,根据牛顿第二定律和运动学公式列式求解,结合简谐运动的知识分析,不难.

 阅读快车系列答案
阅读快车系列答案 质量为m的小球由轻绳a和b分别系于一轻质木架上的A点和C点,如图所示,当轻杆绕轴BC以角速度ω匀速转动时,小球在水平面内做匀速圆周运动,绳a在竖直方向,绳b在水平方向,当小球运动到图示位置时,绳b被烧断的同时杆子停止转动,则下列说法不正确的是( )
质量为m的小球由轻绳a和b分别系于一轻质木架上的A点和C点,如图所示,当轻杆绕轴BC以角速度ω匀速转动时,小球在水平面内做匀速圆周运动,绳a在竖直方向,绳b在水平方向,当小球运动到图示位置时,绳b被烧断的同时杆子停止转动,则下列说法不正确的是( )| A. | 在绳b被烧断瞬间,a绳中张力突然增大 | |
| B. | 小球仍在水平面内做圆周运动 | |
| C. | 小球可能在垂直于平面ABC的竖直平面内摆动 | |
| D. | 小球可能在垂直于平面ABC的竖直平面内做圆周运动 |
| A. | 球与斜槽间有摩擦 | |
| B. | 安装斜槽时其末端不水平 | |
| C. | 建立坐标系时,x轴、y轴正交,但y轴不够竖直 | |
| D. | 根据曲线计算平抛运动初速度时,曲线上取作计算的点离原点O较远 |
| A. | 构成原电池的正极和负极必须是两种不同的金属 | |
| B. | 原电池是将化学能转变为电能的装置 | |
| C. | 在原电池中,电子流出的一极是负极,发生氧化反应 | |
| D. | 原电池放电时,电流的方向是从正极到负极 |
 如图所示,封闭气体A,B的初始温度相同,体积分别为V1,V2,并且V1=2V2,现使两气柱A,B升高相同的温度后,两气柱的体积分别为V1′和V2′,若忽略气体压强的变化,则( )
如图所示,封闭气体A,B的初始温度相同,体积分别为V1,V2,并且V1=2V2,现使两气柱A,B升高相同的温度后,两气柱的体积分别为V1′和V2′,若忽略气体压强的变化,则( )| A. | V1′=2V2′ | B. | V1′>2V2′ | C. | V1′<2V2′ | D. | 无法确定 |

| A. | 通过R的电流iR随时间t变化的规律是iR=$\sqrt{2}$cos100πt A | |
| B. | 在t=0.01s时,电流表A的读数为$\frac{\sqrt{2}}{10}$A | |
| C. | 在t=0.02s时,电压表V的读数为$\sqrt{2}$V | |
| D. | 在t=5s的时间内,流过电阻R的电荷量为0.5C |
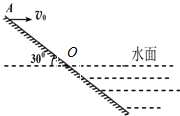 如图所示为湖边一斜坡(倾角为30°)的横截面示意图,水面与斜坡的交点为O.从A点以速度v0沿水平方向扔出一小石块,已知AO=90m,不计空气阻力,下列说法正确的是( )
如图所示为湖边一斜坡(倾角为30°)的横截面示意图,水面与斜坡的交点为O.从A点以速度v0沿水平方向扔出一小石块,已知AO=90m,不计空气阻力,下列说法正确的是( )| A. | 若v0>25m/s,则石块可以落入水中 | |
| B. | 若v0<28m/s,则石块不能落入水中 | |
| C. | 若石块能落入水中,则v0越大,落水时速度方向与水平面的夹角越大 | |
| D. | 若石块能落到斜坡AO上,则不管v0多大,落到斜面上时速度方向与斜面的夹角不变 |
 传送带以v=6m/s的速度顺时针转动,一小物块轻轻放在传送带左端B点,然后在传送带的带动下,从传送带右端的C点水平抛出,最后落到地面上的D点,己知传送带长度 L=18m,物块与传送带之间的动摩擦因数μ=0.3(g=10m/s2).
传送带以v=6m/s的速度顺时针转动,一小物块轻轻放在传送带左端B点,然后在传送带的带动下,从传送带右端的C点水平抛出,最后落到地面上的D点,己知传送带长度 L=18m,物块与传送带之间的动摩擦因数μ=0.3(g=10m/s2).