题目内容
如下图所示，电动机带动橡皮滚轮匀速转动，在滚轮的作用下，可将金属杆沿斜面从最底端A送到汽车车厢中。已知斜面长
AC=2.4 m，车厢高
=1.2 m，金属杆长AB=0.8 m，质量m=1×103 kg,调节控制滚轮的机械，使滚轮对杆的压力为FN=4.2×104 N，滚轮与杆之间的动摩擦因数μ=0.5,滚轮边缘的线速度恒为v=4 m/s，取g=10 m/s2，计算结果保留2位有效数字，斜面光滑。求：
（1）杆匀加速上升的加速度a等于多少？
（2）从杆开始运动到其前端运动到C点所用的时间t等于多少？
解：（1）金属杆受的摩擦力f=μFN
对金属杆应用牛顿第二定律：f-mgsinθ=ma
由图sinθ=
联立解得a=16 m/s2。
（2）金属杆沿斜面匀速上升的位移和时间分别为
x1=m=0.5 m
t1==
s=0.25 s
因为x1＜AB，故杆匀速的位移和时间分别为
x2=AB-x1=0.3 m
t2=
=
s=0.075 s
以后杆匀减速位移x2=
=0.8 m后，其前端到达C点。
杆匀减速的加速度a′=
=5 m/s2
设杆匀速的时间为t2，则
x3=vt-
a′t32
解得t3=0.24 s
所求t=t1+t2+t3=0.57 s。
练习册系列答案
名校课堂系列答案
相关题目
如图所示，电动机带动滚轮B匀速转动，在滚轮的作用下，将金属杆从最底端A送往倾角θ=30°的足够长斜面上部．滚轮中心B与斜面底部A的距离为L=6.5m，当金属杆的下端运动到B处时，滚轮提起，与杆脱离接触．杆由于自身重力作用最终会返回斜面底部，与挡板相撞后，立即静止不动．此时滚轮再次压紧杆，又将金属杆从最底端送往斜面上部，如此周而复始．已知滚轮边缘线速度恒为v=4m/s，滚轮对杆的正压力FN=2×104N，滚轮与杆间的动摩擦因数为μ=0.35，杆的质量为m=1×103Kg，不计杆与斜面间的摩擦，取g=10m/s2．
如图所示，电动机带动滚轮B匀速转动，在滚轮的作用下，将金属杆从最底端A送往倾角θ=30°的足够长斜面上部．滚轮中心B与斜面底部A的距离为L=6.5m，当金属杆的下端运动到B处时，滚轮提起，与杆脱离接触．杆由于自身重力作用最终会返回斜面底部，与挡板相撞后，立即静止不动．此时滚轮马上再次压紧杆，又将金属杆从最底端送往斜面上部，如此周而复始．已知滚轮边缘线速度恒为v=4m/s，滚轮对杆的正压力FN=2×104N，滚轮与杆间的动摩擦因数为μ=0.45，杆的质量为m=1×103Kg，不计杆与斜面间的摩擦，取g=10m/s2．求：
如图所示，电动机带动滚轮做逆时针匀速转动，在滚轮的摩擦力作用下，将一金属板从斜面底端A送往上部，已知斜面光滑且足够长，倾角θ=30°，滚轮与金属板的切点B到斜面底端A的距离为L=6.5m，当金属板的下端运动到切点B处时，立即提起滚轮使它与板脱离接触．已知板之后返回斜面底部与挡板相撞后立即静止，此时放下滚轮再次压紧板，再次将板从最底端送往斜面上部，如此往复．已知板的质量为m=1×103kg，滚轮边缘线速度恒为v=4m/s，滚轮对板的正压力FN=2×104N，滚轮与板间的动摩擦因数为μ=0.35，取g=10m/s2．求：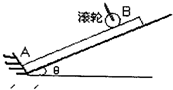
如图所示，电动机带动滚轮做逆时针匀速转动，在滚轮的摩擦力作用下，将一金属板从光滑斜面底端A送往斜面上端，倾角兹=30°，滚轮与金属板的切点B到斜面底端A距离L=6.5m，当金属板的下端运动到切点B处时，立即提起滚轮使其与板脱离．已知板的质量m=1×103kg，滚轮边缘线速度v=4m/s，滚轮对板的正压力FN=2×104N，滚轮与金属板间的动摩擦因数为滋=0.35，取g=10m/s2．求：