题目内容
3. 三根平行的直导线,分别垂直地通过一个等腰直角三角形的三个顶点,如图所示.现使每条通电导线在斜边中点O所产生的磁感应强度的大小均为B,则该处的磁感应强度的大小和方向如何?
三根平行的直导线,分别垂直地通过一个等腰直角三角形的三个顶点,如图所示.现使每条通电导线在斜边中点O所产生的磁感应强度的大小均为B,则该处的磁感应强度的大小和方向如何?
分析 本题考查了磁场的叠加,根据导线周围磁场分布可知,与导线等距离地方磁感应强度大小相等,根据安培定则判断出两导线在A点形成磁场方向,磁感应强度B是矢量,根据矢量分解合成的平行四边形定则求解.
解答 解:根据安培定则,I1与I3在O点处产生的磁感应强度相同,I2在O点处产生的磁感应强度的方向与B1(B3)相垂直,
又知B1、B2、B3的大小相等均为B,
根据矢量的运算法则可知O处的实际磁感应强度大小为:
B合=$\sqrt{{B}^{2}+(2B)^{2}}$=$\sqrt{5}$B,
方向如图,tanθ=$\frac{2B}{B}$=2,
解得:θ=arctan 2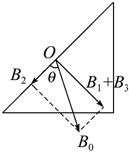
答:该处的磁感应强度的大小为$\sqrt{5}$B;方向在三角形平面内与斜边夹角为arctan 2.
点评 磁感应强度为矢量,合成时要用平行四边形定则,因此要正确根据安培定则判断导线周围磁场方向是解题的前提.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
13.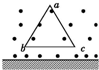 如图所示,有一正三角形铝框abc处在水平向外的非匀强磁场中,场中各点的磁感应强度By=$\frac{{B}_{0}}{y+c}$,y为该点到地面的距离,c为常数,B0为一定值.铝框平面与磁场垂直,底边bc水平(空气阻力不计),将铝框由静止释放,在铝框下落到地面前的过程中( )
如图所示,有一正三角形铝框abc处在水平向外的非匀强磁场中,场中各点的磁感应强度By=$\frac{{B}_{0}}{y+c}$,y为该点到地面的距离,c为常数,B0为一定值.铝框平面与磁场垂直,底边bc水平(空气阻力不计),将铝框由静止释放,在铝框下落到地面前的过程中( )
 如图所示,有一正三角形铝框abc处在水平向外的非匀强磁场中,场中各点的磁感应强度By=$\frac{{B}_{0}}{y+c}$,y为该点到地面的距离,c为常数,B0为一定值.铝框平面与磁场垂直,底边bc水平(空气阻力不计),将铝框由静止释放,在铝框下落到地面前的过程中( )
如图所示,有一正三角形铝框abc处在水平向外的非匀强磁场中,场中各点的磁感应强度By=$\frac{{B}_{0}}{y+c}$,y为该点到地面的距离,c为常数,B0为一定值.铝框平面与磁场垂直,底边bc水平(空气阻力不计),将铝框由静止释放,在铝框下落到地面前的过程中( )| A. | 铝框回路中的磁通量变大,有顺时针方向的感应电流产生 | |
| B. | 回路中的感应电流沿顺时针方向,底边bc两端间的电势差为0 | |
| C. | 铝框下落的加速度大小一定小于重力加速度g | |
| D. | 底边bc受到的安培力向上,折线bac受到的安培力向下,铝框下落时的加速度大小可能等于g |
14.关于斜抛运动的性质以下说法正确的是( )
| A. | 斜抛运动是匀变速运动,因为其速度是恒定的 | |
| B. | 斜抛运动是匀变速运动,因为其加速度是恒定的 | |
| C. | 斜抛运动是非匀变速运动,因为其速度是变化的 | |
| D. | 斜抛运动是非匀变速运动,因为其加速度是变化的 |
18.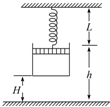 如图所示,一导热性良好的汽缸内用活塞封住一定量的气体(不计活塞与缸壁摩擦),当温度升高时,改变的量有( )
如图所示,一导热性良好的汽缸内用活塞封住一定量的气体(不计活塞与缸壁摩擦),当温度升高时,改变的量有( )
 如图所示,一导热性良好的汽缸内用活塞封住一定量的气体(不计活塞与缸壁摩擦),当温度升高时,改变的量有( )
如图所示,一导热性良好的汽缸内用活塞封住一定量的气体(不计活塞与缸壁摩擦),当温度升高时,改变的量有( )| A. | 活塞高度h | B. | 汽缸底距地面高度H | ||
| C. | 气体压强p | D. | 弹簧长度L |
8.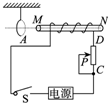 如图所示装置中,闭合铜环A静止悬挂在通电螺线管的M端,螺线管的轴线垂直于环面并正对环心.要使铜环向螺线管靠近,下列各操作中可以实现的是( )
如图所示装置中,闭合铜环A静止悬挂在通电螺线管的M端,螺线管的轴线垂直于环面并正对环心.要使铜环向螺线管靠近,下列各操作中可以实现的是( )
 如图所示装置中,闭合铜环A静止悬挂在通电螺线管的M端,螺线管的轴线垂直于环面并正对环心.要使铜环向螺线管靠近,下列各操作中可以实现的是( )
如图所示装置中,闭合铜环A静止悬挂在通电螺线管的M端,螺线管的轴线垂直于环面并正对环心.要使铜环向螺线管靠近,下列各操作中可以实现的是( )| A. | 开关S由断开到接通的瞬间 | B. | 开关S由接通到断开的瞬间 | ||
| C. | 将滑片P向C滑动的过程中 | D. | 将滑片P向D滑动的过程中 |
12.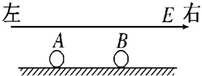 如图,光滑绝缘水平面上带异号电荷的小球 A、B,它们一起在水平向右的匀强电场中 向右做匀加速运动,且保持相对静止.设小球 A 的带电荷量大小为 QA,小球 B的带电荷量大 小为 QB,下列判断正确的是( )
如图,光滑绝缘水平面上带异号电荷的小球 A、B,它们一起在水平向右的匀强电场中 向右做匀加速运动,且保持相对静止.设小球 A 的带电荷量大小为 QA,小球 B的带电荷量大 小为 QB,下列判断正确的是( )
 如图,光滑绝缘水平面上带异号电荷的小球 A、B,它们一起在水平向右的匀强电场中 向右做匀加速运动,且保持相对静止.设小球 A 的带电荷量大小为 QA,小球 B的带电荷量大 小为 QB,下列判断正确的是( )
如图,光滑绝缘水平面上带异号电荷的小球 A、B,它们一起在水平向右的匀强电场中 向右做匀加速运动,且保持相对静止.设小球 A 的带电荷量大小为 QA,小球 B的带电荷量大 小为 QB,下列判断正确的是( )| A. | 小球 A带正电,小球 B带负电,且 QA>QB | |
| B. | 小球 A带正电,小球 B带负电,且 QA<QB | |
| C. | 小球 A带负电,小球 B带正电,且 QA>QB | |
| D. | 小球 A带负电,小球 B带正电,且 QA<QB |
13.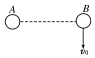 如图所示,把一个带电小球A固定在光滑的水平绝缘桌面上,在桌面的另一处放置带电小球B.现给B一个沿垂直AB方向的速度v0,B球将( )
如图所示,把一个带电小球A固定在光滑的水平绝缘桌面上,在桌面的另一处放置带电小球B.现给B一个沿垂直AB方向的速度v0,B球将( )
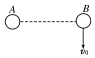 如图所示,把一个带电小球A固定在光滑的水平绝缘桌面上,在桌面的另一处放置带电小球B.现给B一个沿垂直AB方向的速度v0,B球将( )
如图所示,把一个带电小球A固定在光滑的水平绝缘桌面上,在桌面的另一处放置带电小球B.现给B一个沿垂直AB方向的速度v0,B球将( )| A. | 若A、B为异种电荷,B球可能做圆周运动 | |
| B. | 若A、B为异种电荷,B球一定做加速度、速度均变小的曲线运动 | |
| C. | 若A、B为同种电荷,B球一定做远离A的变加速曲线运动 | |
| D. | 若A、B为同种电荷,B球的动能一定会减小 |