题目内容
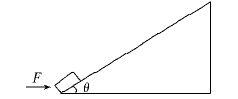
如图17所示,质量为M的劈块,其左右劈面的倾角分别为θ1 = 30°、θ2 = 45°,质量分别为m1 = kg和m2 = 2.0kg的两物块,同时分别从左右劈面的顶端从静止开始下滑,劈块始终与水平面保持相对静止,各相互接触面之间的动摩擦因数均为μ =" 0.20" ,求两物块下滑过程中(m1和m2均未达到底端)劈块受到地面的摩擦力。(g = 10m/s2)
kg和m2 = 2.0kg的两物块,同时分别从左右劈面的顶端从静止开始下滑,劈块始终与水平面保持相对静止,各相互接触面之间的动摩擦因数均为μ =" 0.20" ,求两物块下滑过程中(m1和m2均未达到底端)劈块受到地面的摩擦力。(g = 10m/s2)
17.
 kg和m2 = 2.0kg的两物块,同时分别从左右劈面的顶端从静止开始下滑,劈块始终与水平面保持相对静止,各相互接触面之间的动摩擦因数均为μ =" 0.20" ,求两物块下滑过程中(m1和m2均未达到底端)劈块受到地面的摩擦力。(g = 10m/s2)
kg和m2 = 2.0kg的两物块,同时分别从左右劈面的顶端从静止开始下滑,劈块始终与水平面保持相对静止,各相互接触面之间的动摩擦因数均为μ =" 0.20" ,求两物块下滑过程中(m1和m2均未达到底端)劈块受到地面的摩擦力。(g = 10m/s2)17.

-2.3N负号表示整体在水平方向受到的合外力的方向与选定的正方向相反。所以劈块受到地面的摩擦力的大小为2。3N,方向水平向右。
选M 、m1和m2构成的整体为研究对象,把在相同时间内,M保持静止,m1和m2分别以不同的加速度下滑三个过程视为一个整体过程来研究。根据各种性质的力产生的条件,在水平方向,整体除受到地面的静摩擦力外,不可能再受到其他力;如果受到静摩擦力,那么此力便是整体在水平方向受到的合外力。
根据系统牛顿第二定律,取水平向左的方向为正方向,则有:
F合x = Ma′+ m1a1x-m2a2x
其中a′、a1x和a2x分别为M 、m1和m2在水平方向的加速度的大小,而
a′=" 0" ,a1x =" g" (sin30°-μcos30°)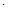 cos30° ,a2x =" g" (sin45°-μcos45°)
cos30° ,a2x =" g" (sin45°-μcos45°) 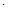 cos45° 。所以:
cos45° 。所以:
F合 =" m1g" (sin30°-μcos30°)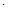 cos30°-m2g (sin45°-μcos45°)
cos30°-m2g (sin45°-μcos45°) 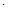 cos45° =
cos45° = ×10×(
×10×(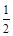 -0.2×
-0.2×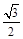 )×
)×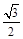 -2.0×10×(
-2.0×10×(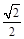 -0.3×
-0.3×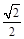 )×
)×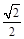 =-2.3N
=-2.3N
负号表示整体在水平方向受到的合外力的方向与选定的正方向相反。所以劈块受到地面的摩擦力的大小为2。3N,方向水平向右。
本题考查整体隔离法的应用,静止时现已整体为研究对象,所以整体没有运动趋势,不受摩擦力作用,两物块下滑过程中,分析两物块的受力情况,把加速度分解为水平和竖直方向,由牛顿第二定律列公式可求得水平方向的合力,由此可知要想静止不动,静摩擦力必须平衡该力
根据系统牛顿第二定律,取水平向左的方向为正方向,则有:
F合x = Ma′+ m1a1x-m2a2x
其中a′、a1x和a2x分别为M 、m1和m2在水平方向的加速度的大小,而
a′=" 0" ,a1x =" g" (sin30°-μcos30°)
 cos30° ,a2x =" g" (sin45°-μcos45°)
cos30° ,a2x =" g" (sin45°-μcos45°) 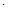 cos45° 。所以:
cos45° 。所以:F合 =" m1g" (sin30°-μcos30°)
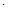 cos30°-m2g (sin45°-μcos45°)
cos30°-m2g (sin45°-μcos45°) 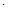 cos45° =
cos45° = ×10×(
×10×(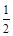 -0.2×
-0.2×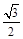 )×
)×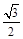 -2.0×10×(
-2.0×10×(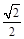 -0.3×
-0.3×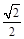 )×
)×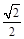 =-2.3N
=-2.3N负号表示整体在水平方向受到的合外力的方向与选定的正方向相反。所以劈块受到地面的摩擦力的大小为2。3N,方向水平向右。
本题考查整体隔离法的应用,静止时现已整体为研究对象,所以整体没有运动趋势,不受摩擦力作用,两物块下滑过程中,分析两物块的受力情况,把加速度分解为水平和竖直方向,由牛顿第二定律列公式可求得水平方向的合力,由此可知要想静止不动,静摩擦力必须平衡该力

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

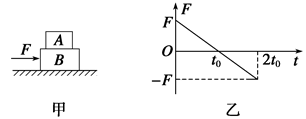



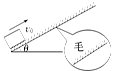
 ,一滑块以初速度v0="16" m/s从底端A点滑上斜面,滑至B点后又返回到A点.滑块运动的图象如图乙所示,求:(已知:
,一滑块以初速度v0="16" m/s从底端A点滑上斜面,滑至B点后又返回到A点.滑块运动的图象如图乙所示,求:(已知: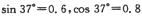 ,重力加速度g="10" m/s2)
,重力加速度g="10" m/s2)