题目内容
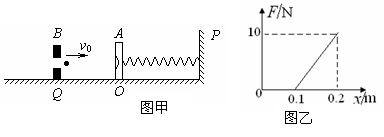
如图甲所示,质量M=0.040kg的靶盒A静止在光滑水平导轨上的O点,水平轻质弹簧一端栓在固定挡板P上,另一端与靶盒A连接。Q处有一固定的发射器B,它可以瞄准靶盒发射一颗水平速度为v0=50m/s,质量m=0.010kg的弹丸,当弹丸打入靶盒A后,便留在盒内,碰撞时间极短。已知弹簧的弹性势能可表示为Ep=![]() kx2,弹簧的弹力随弹簧长度x变化的图象如图乙所示,不计空气阻力。求:
kx2,弹簧的弹力随弹簧长度x变化的图象如图乙所示,不计空气阻力。求:
①弹丸打入靶盒A过程中弹丸损失的机械能。
②弹丸进入靶盒A后,靶盒A的最大位移。
![]()
【解题思路】:①弹丸打入靶盒A过程,由动量守恒定律
mv0=(M+m)v,
解得:v=10m/s。(2分)
弹丸损失的机械能:△E= ![]() mv02-
mv02- ![]() mv2=
mv2=![]() m(v02- v2)=12J。(2分)
m(v02- v2)=12J。(2分)
② 靶盒A的速度减为零时,弹簧的弹性势能最大,由系统机械能守恒得
Ep= ![]() (M+m)v2=2.5J,(2分)
(M+m)v2=2.5J,(2分)

![]()

练习册系列答案
相关题目
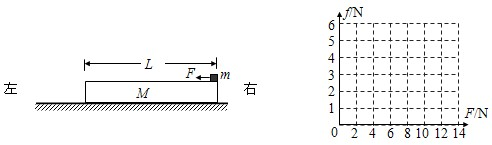
 如图甲所示,质量m=1kg的小球放在光滑的水平面上,在界线MN的左方始终受到水平恒力F1的作用,在MN的右方除受F1外还受到与F1在同条直线上的水平恒力F2的作用.小球从A点由静止开始运动,运动的v-t图象如图乙所示.由图可知,下列说法中正确的是( )
如图甲所示,质量m=1kg的小球放在光滑的水平面上,在界线MN的左方始终受到水平恒力F1的作用,在MN的右方除受F1外还受到与F1在同条直线上的水平恒力F2的作用.小球从A点由静止开始运动,运动的v-t图象如图乙所示.由图可知,下列说法中正确的是( )

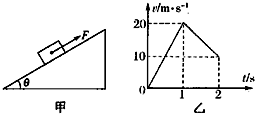 如图甲所示,质量m=1.0kg的物体置于倾角θ=37°的固定粗糙斜面上,t=0时对物体施以平行于斜面向上的拉力F,t1=1s时撤去拉力,物体运动的部分v-t图象如图乙所示.设斜面足够长,物体所受最大静摩擦力与滑动摩擦力大小相等,求拉力F的大小及物块能上升的最大高度(sin37°=0.6,cos37°=0.8,g取10m/s2)
如图甲所示,质量m=1.0kg的物体置于倾角θ=37°的固定粗糙斜面上,t=0时对物体施以平行于斜面向上的拉力F,t1=1s时撤去拉力,物体运动的部分v-t图象如图乙所示.设斜面足够长,物体所受最大静摩擦力与滑动摩擦力大小相等,求拉力F的大小及物块能上升的最大高度(sin37°=0.6,cos37°=0.8,g取10m/s2)