题目内容
 如图所示,重力为G的光滑球卡在槽中,球与槽的A、B两点接触,其中A与球心O的连线AO与竖直方向的夹角θ=30°.若球对A、B两点的压力大小分别为NA、NB,则
如图所示,重力为G的光滑球卡在槽中,球与槽的A、B两点接触,其中A与球心O的连线AO与竖直方向的夹角θ=30°.若球对A、B两点的压力大小分别为NA、NB,则
- A.
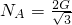

- B.NA=2G
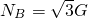
- C.
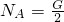

- D.
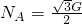
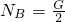
A
分析:分析小球受力情况,作出力图,根据平衡条件求解球受到的A、B两点的支持力,由牛顿第三定律即可得到球对A、B两点的压力大小分别为NA、NB.
解答:分析小球受力情况:重力G、A点的支持力NA′和B点的支持力NB′,根据平衡条件得知,NA′和NB′的合力F与重力G等大、反向,即F=G.由图可得: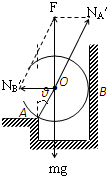
NA′= =
=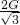
NB′=Ftan30°=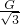
根据牛顿第三定律可知,球对A、B两点的压力大小分别为NA=NA′=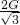 ,NB=NB′=
,NB=NB′=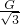 .
.
故选A
点评:本题是简单的三力平衡问题,分析受力,作出力图是解题的关键,根据受力时,要抓住A、B对球的弹力都通过球心.
分析:分析小球受力情况,作出力图,根据平衡条件求解球受到的A、B两点的支持力,由牛顿第三定律即可得到球对A、B两点的压力大小分别为NA、NB.
解答:分析小球受力情况:重力G、A点的支持力NA′和B点的支持力NB′,根据平衡条件得知,NA′和NB′的合力F与重力G等大、反向,即F=G.由图可得:
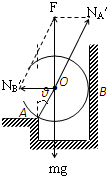
NA′=
 =
=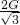
NB′=Ftan30°=
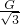
根据牛顿第三定律可知,球对A、B两点的压力大小分别为NA=NA′=
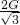 ,NB=NB′=
,NB=NB′=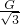 .
.故选A
点评:本题是简单的三力平衡问题,分析受力,作出力图是解题的关键,根据受力时,要抓住A、B对球的弹力都通过球心.

练习册系列答案
相关题目
 如图所示,重力为G的均匀球,用绳系在光滑的墙面上.如果所用的绳子变长,则墙所受的压力将
如图所示,重力为G的均匀球,用绳系在光滑的墙面上.如果所用的绳子变长,则墙所受的压力将 如图所示,重力为G的物体放在倾角为θ的固定斜面上,静止不动.下面说法正确的是( )
如图所示,重力为G的物体放在倾角为θ的固定斜面上,静止不动.下面说法正确的是( ) 如图所示,重力为G的物体与地面的动摩擦因数为μ.现用绳子拉物体,绳子与水平面成45°角.若要拉动物体,绳的拉力F至少为( )
如图所示,重力为G的物体与地面的动摩擦因数为μ.现用绳子拉物体,绳子与水平面成45°角.若要拉动物体,绳的拉力F至少为( )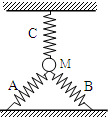 如图所示,重力为G的质点M,与三根劲度系数相同的螺旋弹簧A、B、c相连,C处于竖直方向,静止时,相邻弹簧间的夹角均为120°,已知弹簧A和B对质点的作用力的大小均为2G,则弹簧C对质点的作用力的大小可能为( )
如图所示,重力为G的质点M,与三根劲度系数相同的螺旋弹簧A、B、c相连,C处于竖直方向,静止时,相邻弹簧间的夹角均为120°,已知弹簧A和B对质点的作用力的大小均为2G,则弹簧C对质点的作用力的大小可能为( )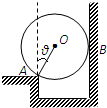 如图所示,重力为G的光滑球卡在槽中,球与槽的A、B两点接触,其中A与球心O的连线AO与竖直方向的夹角θ=30°.若球对A、B两点的压力大小分别为NA、NB,则( )
如图所示,重力为G的光滑球卡在槽中,球与槽的A、B两点接触,其中A与球心O的连线AO与竖直方向的夹角θ=30°.若球对A、B两点的压力大小分别为NA、NB,则( )