��Ŀ����
 ��ͼ��ʾ������ֱƽ��xOy�ڣ�x���·������㹻�����ǿ�糡���糡ǿ��ΪE��������ֱ���£�ͬʱ���ڷ���ֱֽ���������ǿ�ų�����һ������С���y����A��0��L�����Դ�СΪv0ˮƽ�ٶ�ƽ�׳�ȥ��v0 δ֪����С��x����C�㣨2L��0����ǡ��������Բ���˶��������ų��������ٴη���A�㣮���������ٶ�Ϊg�������������ƣ�
��ͼ��ʾ������ֱƽ��xOy�ڣ�x���·������㹻�����ǿ�糡���糡ǿ��ΪE��������ֱ���£�ͬʱ���ڷ���ֱֽ���������ǿ�ų�����һ������С���y����A��0��L�����Դ�СΪv0ˮƽ�ٶ�ƽ�׳�ȥ��v0 δ֪����С��x����C�㣨2L��0����ǡ��������Բ���˶��������ų��������ٴη���A�㣮���������ٶ�Ϊg�������������ƣ���1���ж�С������绹�Ǵ����磬��������С����˶��켣
��2�������С��ij��ٶ�v0�Ĵ�С
��3����ų��ĴŸ�Ӧǿ��B�Ĵ�С
��4����С���A��������ٴλص�A�����õ�ʱ�䣮
��������1������С��������Բ���˶�������������糡����ƽ�⣬������⣻
��2������ƽ���˶��Ĺ��ɣ������˶��ĺϳ���ֽ⣬����˶�ѧ��ʽ��������⣻
��3������λ�ƹ�ʽ���뼸�ι�ϵ��ţ�ٵڶ����ɣ�������⣻
��4������С����ƽ���˶������˶�ѧ��ʽ������˶�ʱ�䣻��������Բ���˶���������ڹ�ʽ��Բ�Ľǣ�����˶�ʱ�䣬��������ʱ�䣮
��2������ƽ���˶��Ĺ��ɣ������˶��ĺϳ���ֽ⣬����˶�ѧ��ʽ��������⣻
��3������λ�ƹ�ʽ���뼸�ι�ϵ��ţ�ٵڶ����ɣ�������⣻
��4������С����ƽ���˶������˶�ѧ��ʽ������˶�ʱ�䣻��������Բ���˶���������ڹ�ʽ��Բ�Ľǣ�����˶�ʱ�䣬��������ʱ�䣮
��� �⣺��1��С��x ���ǡ��������Բ���˶�����qE=mg��С������磮
�⣺��1��С��x ���ǡ��������Բ���˶�����qE=mg��С������磮
����С���˶��Ĺ��ʾ��ͼ��
��2����ƽ���˶��Ĺ��ɿ�֪��
2L=v0t
L=
gt2
���v0=
��3����С��C��ʱ���ٶ�Ϊv��
��A��C��2L=
t��L=
t��
v=
v0
�ٶȷ�����x���������45������
���ݼ��ι�ϵ��r=2
L
��C��D������ţ�ٵڶ�����qvB=m
��ã�B=
=
��
��4����A��C��С���һ�ξ���x�ᣬ����ʱ��Ϊt1=
��C��D��С��ڶ��ξ���x�ᣬ
����ʱ��Ϊt2��T=
��t2=
=
С���A����������ٴη���A���ʱ�䣺t=2t1+t2=2
+3��
��1���ж�С������磬���С����˶��켣����ͼ��ʾ��
��2�������С��ij��ٶ�v0�Ĵ�Сv0=
��
��3����ų��ĴŸ�Ӧǿ��B�Ĵ�С
��
��4����С���A��������ٴλص�A�����õ�ʱ��2
+3��
��
 �⣺��1��С��x ���ǡ��������Բ���˶�����qE=mg��С������磮
�⣺��1��С��x ���ǡ��������Բ���˶�����qE=mg��С������磮����С���˶��Ĺ��ʾ��ͼ��
��2����ƽ���˶��Ĺ��ɿ�֪��
2L=v0t
L=
| 1 |
| 2 |
���v0=
| 2gL |
��3����С��C��ʱ���ٶ�Ϊv��
��A��C��2L=
| v | 0 |
| 0+vy |
| 2 |
v=
| 2 |
�ٶȷ�����x���������45������
���ݼ��ι�ϵ��r=2
| 2 |
��C��D������ţ�ٵڶ�����qvB=m
| v2 |
| r |
��ã�B=
| v0E |
| 2gL |
| E | ||
|
��4����A��C��С���һ�ξ���x�ᣬ����ʱ��Ϊt1=
|
��C��D��С��ڶ��ξ���x�ᣬ
����ʱ��Ϊt2��T=
| 2��m |
| qB |
| 3T |
| 4 |
| 3��E |
| 2gB |
С���A����������ٴη���A���ʱ�䣺t=2t1+t2=2
|
|
��1���ж�С������磬���С����˶��켣����ͼ��ʾ��
��2�������С��ij��ٶ�v0�Ĵ�Сv0=
| 2gL |
��3����ų��ĴŸ�Ӧǿ��B�Ĵ�С
| E | ||
|
��4����С���A��������ٴλص�A�����õ�ʱ��2
|
|
����������С��������Բ���˶�����������������С����ƽ���˶����˶����������մ���ƽ���˶��Ĺ��ɣ���ע�⼸�ι�ϵ�����е�Ӧ�ã�

��ϰ��ϵ�д�
�����Ŀ
 ��2008?���ݶ�ģ����ͼ��ʾ������ֱƽ������ˮƽ���ҵ���ǿ�糡��ͬһ��ֱƽ����ˮƽ��ֱ�ľ�Եϸ��һ��ϵһ�������С����һ�˹̶���0�㣬��֪����С���ܵ��ĵ糡������������С���ɾ�ֹ�ͷţ�����ͼ����ֱ����ǰС������������
��2008?���ݶ�ģ����ͼ��ʾ������ֱƽ������ˮƽ���ҵ���ǿ�糡��ͬһ��ֱƽ����ˮƽ��ֱ�ľ�Եϸ��һ��ϵһ�������С����һ�˹̶���0�㣬��֪����С���ܵ��ĵ糡������������С���ɾ�ֹ�ͷţ�����ͼ����ֱ����ǰС������������ ��ͼ��ʾ������ֱƽ������һ�߳�ΪL�������������ڳ�ǿΪE����ǿ�糡�У��糡������������һ��ƽ�У�һ����Ϊm��������Ϊq��С����ijһ�ߵ��е㣬�Դ�ֱ�ڸñߵ�ˮƽ����V0���������������С���ٴ��˶���������������ı�Եʱ�����еĶ��ܿ���Ϊ��������
��ͼ��ʾ������ֱƽ������һ�߳�ΪL�������������ڳ�ǿΪE����ǿ�糡�У��糡������������һ��ƽ�У�һ����Ϊm��������Ϊq��С����ijһ�ߵ��е㣬�Դ�ֱ�ڸñߵ�ˮƽ����V0���������������С���ٴ��˶���������������ı�Եʱ�����еĶ��ܿ���Ϊ�������� ��ͼ��ʾ������ֱƽ������һ��Բ�ι����Բ��ΪO��һ�ʵ�С�����Բ�ĵȸߵ�Բ�ι���ϵ�A�����ٶ�v0ˮƽ�����׳�������Բ����ϵ�C�㣬��֪OC��������OA�ļн�Ϊ�ȣ���С���A��C��ʱ��t=���������������ƣ�
��ͼ��ʾ������ֱƽ������һ��Բ�ι����Բ��ΪO��һ�ʵ�С�����Բ�ĵȸߵ�Բ�ι���ϵ�A�����ٶ�v0ˮƽ�����׳�������Բ����ϵ�C�㣬��֪OC��������OA�ļн�Ϊ�ȣ���С���A��C��ʱ��t=���������������ƣ�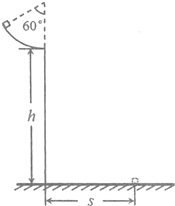 ��ͼ��ʾ������ֱƽ������һ���ֲڵ�
��ͼ��ʾ������ֱƽ������һ���ֲڵ�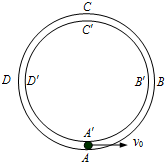 ��ͼ��ʾ������ֱƽ���ڹ̶������ܿ�����ͬ��Բ�ι��������ABCD�⻬���ڹ��A��B��C��D����ϰ벿��B��C��D��ֲڣ��°벿��B��A��D��⻬��һ����m=0.2kg��С��ӹ������͵�A���Գ��ٶ�v0�����˶�����ijߴ���С����Բ��࣬��֪Բ�ι���İ뾶R=0.32m��ȡg=10m/s2��
��ͼ��ʾ������ֱƽ���ڹ̶������ܿ�����ͬ��Բ�ι��������ABCD�⻬���ڹ��A��B��C��D����ϰ벿��B��C��D��ֲڣ��°벿��B��A��D��⻬��һ����m=0.2kg��С��ӹ������͵�A���Գ��ٶ�v0�����˶�����ijߴ���С����Բ��࣬��֪Բ�ι���İ뾶R=0.32m��ȡg=10m/s2��