题目内容
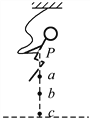
【题目】如图,一固定的楔形木块,其斜面的倾角θ=30°,另一边与地面垂直,顶上有一定滑轮.一柔软的轻细线跨过定滑轮,两端分别与物块A和B连接,A、B质量分别为4kg和1kg.开始时将B按在地面上不动,然后放开手让A沿斜面下滑而B上升.物块A与斜面间无摩擦,g取10m/s2.当A沿斜面下滑1m距离时细线突然断了,则( )

A. 细线断裂前A的加速度为5m/s2
B. 细线断裂时A的速度为2m/s
C. 细线断裂前的拉力为10N
D. 放开手后B上升的最大高度为0.2m
【答案】B
【解析】细线断裂前,根据牛顿第二定律,对A:mAgsin30°T=mAa,对B:TmBg=mBa
代入数据:40×![]() T=4a;T-10=a,联立得:a=2m/s2,T=12N,故AC错误;根据v2-v02=2ax,有v2=2×2×1,解得:v=2m/s,即细线断裂时A的速度为2m/s,故B正确;细线断裂后,B只受重力做竖直上抛运动,
T=4a;T-10=a,联立得:a=2m/s2,T=12N,故AC错误;根据v2-v02=2ax,有v2=2×2×1,解得:v=2m/s,即细线断裂时A的速度为2m/s,故B正确;细线断裂后,B只受重力做竖直上抛运动, ![]() ,所以放开手后B上升的最大高度H=h+h′=1+0.2=1.2m,故D错误;故选B.
,所以放开手后B上升的最大高度H=h+h′=1+0.2=1.2m,故D错误;故选B.

练习册系列答案
相关题目