Question

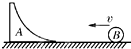
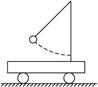
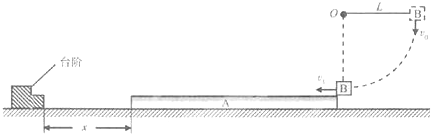
如图，木板A静止在光滑水平面上，其左端固定台阶相距x，与滑块B（可视为质点）相连的细线一端固定在O点．水平拉直细线使滑块由静止释放，当B到达最低点时，细线断牙，B恰好从A右端上表面水平滑入．A与台阶碰撞无机械能损失，不计空气阻力．已知A的质量为2m，B的质量为m，A、B之间动摩擦因数为μ=0.3，细线长为L=0.45m；且A足够长，B不会从A脱离；重力加速度为g．
（1）求细线被拉断瞬间B的速度大小v₁
（2）A与台阶发生碰撞前瞬间，A、B刚好共速，求x为多少？
（3）在满足（2）条件下，A与台阶碰撞后最终的速度为多少．

Answer 1

（1）滑块B到达最低点时速度为v₁，对于B向下摆动过程，由机械能守恒定律得：
mgL=

1

2

m

v

21

代人数据解得：v₁=

2gL

=

2×10×0.45

m/s=3m/s
（2）设A和B共速的速度为v₂．
B在A上滑行过程，以A与B组成的系统为研究对象，取向左方向为正方向，根据动量守恒定律得：
mv₁=3mv₂，
解得：v₂=

1

3

v₁=

1

3

×3m/s=1m/s
A在B上滑动过程中，根据动能定理有：
μmgx=

1

2

?2m

v

22

-0
解得：x=

v 22

μg

=

12

0.3×10

m=

1

3

m；
（3）A与台阶碰撞后最终的速度为v，取向右为正方向，对AB系统，由动量守恒定律有：
2mv₂-mv₂=3mv
解得：v=

2v2-v2

3

=

2×1-1

3

m/s=

1

3

m/s，方向向右．
答：
（1）细线被拉断瞬间B的速度大小v₁为3m/s．
（2）A与台阶发生碰撞前瞬间，A、B刚好共速，x为

1

3

m．
（3）在满足（2）条件下，A与台阶碰撞后最终的速度为

1

3

m/s．