题目内容
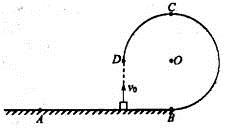
(17分)如图所示,真空中的矩形abcd区域内存在竖直向下的匀强电场,半径为R的圆形区域内同时存在垂直于纸面向里的匀强磁场,磁感应强度为B,圆形边界分别相切于ad、bc边的中点e、f。一带电粒子以初速度v0沿着ef方向射入该区域后能做直线运动;当撤去磁场并保留电场,粒子以相同的初速度沿着ef方向射入恰能从c点飞离该区域。已知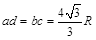 ,忽略粒子的重力。求:
,忽略粒子的重力。求: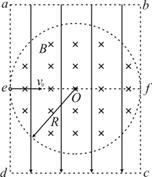
(1)带电粒子的电荷量q与质量m的比值 ;
;
(2)若撤去电场保留磁场,粒子离开矩形区域时的位置。
(1)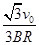 (2)ab边距离b点
(2)ab边距离b点
解析试题分析:(1)设匀强电场强度为E,当电场和磁场同时存在时,粒子沿ef方向做直线运动,有: ①
①
当撤去磁场,保留电场时,粒子恰能从c点飞出,有: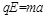 ②
②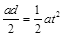 ③
③ ④
④
联解①②③④得: ⑤
⑤
(2)若撤去电场保留磁场,粒子将在洛伦兹力作用下做匀速圆周运动,轨迹如图所示。 ⑥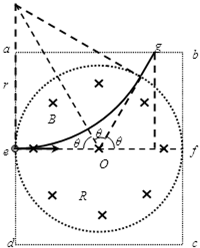
设粒子离开矩形区域时的位置g离b的距离为x,则由牛顿第二定律: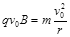 ⑦
⑦
由图中几何关系得: ⑧
⑧ ⑨
⑨
联解⑦⑧⑨得: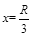 ⑩
⑩
考点:带电粒子在复合场(电场磁场)中的运动 牛顿第二定律 平抛运动

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
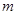 的小球,以初速度
的小球,以初速度 沿轨道向上运动,求:
沿轨道向上运动,求: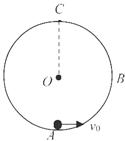
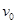 大小可调节,小球在运动过程中出现脱轨现象,则
大小可调节,小球在运动过程中出现脱轨现象,则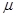 )。某时刻观察到细线偏离竖直方向
)。某时刻观察到细线偏离竖直方向 角,
角,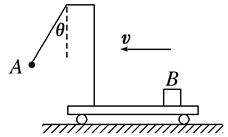

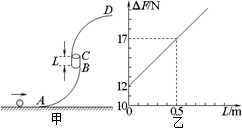
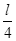 、质量为m的小球用两根不可伸长的轻绳a、b连接,两轻绳的另一端系在一根竖直杆的A、B两点上,A、 B两点相距为l,当两轻绳伸直后,A、B两点到球心的距离均为l。当竖直杆以自己为轴转动并达到稳定时(细绳a、b与杆在同一竖直平面内)。求:
、质量为m的小球用两根不可伸长的轻绳a、b连接,两轻绳的另一端系在一根竖直杆的A、B两点上,A、 B两点相距为l,当两轻绳伸直后,A、B两点到球心的距离均为l。当竖直杆以自己为轴转动并达到稳定时(细绳a、b与杆在同一竖直平面内)。求: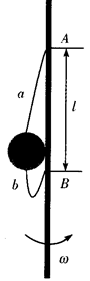
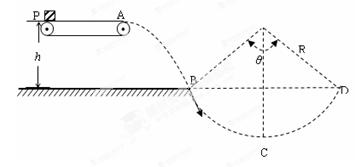

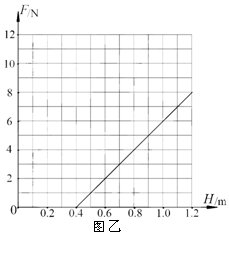
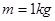 的小物块,从水平面上以速度
的小物块,从水平面上以速度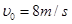 竖直向上抛出,物块从D点进入圆轨道,最终停在A点,物块与水平面间的动摩擦因数
竖直向上抛出,物块从D点进入圆轨道,最终停在A点,物块与水平面间的动摩擦因数 =0.4,取
=0.4,取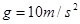 .求:
.求: