题目内容
如图所示,现有一质量为m、电荷量为e的电子从y轴上的P(0,a)点以初速度v0平行于x轴射出,为了使电子能够经过x轴上的Q(b,0)点,可在y轴右侧加一垂直于xOy平面向里、宽度为L的匀强磁场,磁感应强度大小为B,该磁场左、右边界与y轴平行,上、下足够宽(图中未画出).已知
解:设电子在磁场中做圆周运动的轨道半径为r,则eBv0=m![]() ①
①
解得r=![]() ②
②
(1)当r>L时,磁场区域及电子运动轨迹如下图所示,由几何关系有sinθ=![]() ③
③

则磁场左边界距坐标原点的距离为
x1=b-L-[a-r(1-cosθ)]cotθ ④
x1=b-L-[a-![]() (1-cosθ)]cotθ(其中θ=?arcsin
(1-cosθ)]cotθ(其中θ=?arcsin![]() ) ⑤
) ⑤
(2)当r≤L时,磁场区域及电子运动轨迹如下图所示,由几何关系得磁场左边界距坐标原点的距离为

x2=b-![]() ⑥
⑥
解得x2=b-![]() . ⑦
. ⑦

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
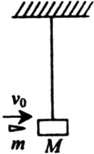 用长为L的细线悬挂一质量为M的小木块,木块静止,如图所示.现有一质量为m的子弹自左方水平地射穿木块,穿透前后子弹的速度分别为v0和v,求子弹穿透木块瞬间细线对木块的拉力.(设子弹穿过木块的时间很短,可不计)
用长为L的细线悬挂一质量为M的小木块,木块静止,如图所示.现有一质量为m的子弹自左方水平地射穿木块,穿透前后子弹的速度分别为v0和v,求子弹穿透木块瞬间细线对木块的拉力.(设子弹穿过木块的时间很短,可不计)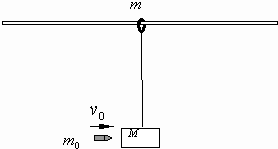 在固定的光滑水平杆(杆足够长)上,套有一个质量m=0.5kg的光滑金属圆环,
在固定的光滑水平杆(杆足够长)上,套有一个质量m=0.5kg的光滑金属圆环,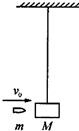 (2012?广东模拟)用不可伸长的细线悬挂一质量为M的小木块,木块静止,如图所示.现有一质量为m的子弹自左方水平地射向木块并停留在木块中,子弹初速度为v0,求:
(2012?广东模拟)用不可伸长的细线悬挂一质量为M的小木块,木块静止,如图所示.现有一质量为m的子弹自左方水平地射向木块并停留在木块中,子弹初速度为v0,求: 在空间中同时存在匀强磁场和匀强电场,匀强电场方向竖直向上,场强大小为E,匀强磁场的方向和大小均未知,如图所示.现有一质量为m的带电小球,用长为L的绝缘线悬挂在一点,小球在水平面上以角速度ω做匀速圆周运动,顺着电场强方向观察,小球向顺时针方向旋转,这时线与竖直方向夹角为θ,线上拉力为零.下列说法正确的是( )
在空间中同时存在匀强磁场和匀强电场,匀强电场方向竖直向上,场强大小为E,匀强磁场的方向和大小均未知,如图所示.现有一质量为m的带电小球,用长为L的绝缘线悬挂在一点,小球在水平面上以角速度ω做匀速圆周运动,顺着电场强方向观察,小球向顺时针方向旋转,这时线与竖直方向夹角为θ,线上拉力为零.下列说法正确的是( )