题目内容
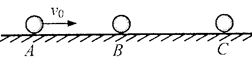
在光滑的水平面上,质量为m1的小球A以速率v0向右运动.在小球A的前方O点有一质量为m2的小球B处于静止状态,如图所示.小球A与小球B发生正碰后小球A、B均向右运动.小球B被在Q点处的墙壁弹回后与小球A在P点相遇,PQ=1.5PO.假设小球间的碰撞及小球与墙壁之间的碰撞都是弹性的,求两小球碰撞后的速度大小之比及质量之比m1∶m2. 
2∶1.
解析试题分析:从两小球碰撞后到它们再次相遇,小球A和B的速度大小保持不变.根据它们通过的路程,可知小球B和小球A在碰撞后的速度大小之比为4∶1。设碰撞后小球A和B的速度分别为v1′和v2′,在碰撞过程中动量守恒,碰撞前后动能相等,则有
m1v1=m1v1′+m2v2′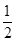 m1v12=
m1v12=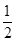 m1v1′2+
m1v1′2+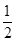 m2v2′2
m2v2′2
得v1′=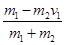
v2′=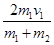
利用v2′:v1′=4:1,
可解出m1∶m2=2∶1.
考点:碰撞问题及动量守恒定律的应用。

练习册系列答案
相关题目
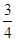 ,则抛出第四个沙包后,此车的运动情况如何?
,则抛出第四个沙包后,此车的运动情况如何? 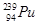 静止时衰变为铀核激发态
静止时衰变为铀核激发态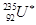 和
和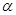 粒子,而铀核激发态
粒子,而铀核激发态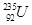 ,并放出能量为0.097MeV的
,并放出能量为0.097MeV的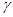 光子。衰变放出的光子的动量可忽略.已知:
光子。衰变放出的光子的动量可忽略.已知: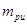 =239.0521u、
=239.0521u、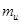 =235.0439u和
=235.0439u和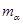 ="4.0026u" ,1u相当于931.5MeV
="4.0026u" ,1u相当于931.5MeV
 的光滑水平圆形轨道,过圆心
的光滑水平圆形轨道,过圆心 相垂直的两虚线交圆弧于A、B、C、D四点,质量为
相垂直的两虚线交圆弧于A、B、C、D四点,质量为 的乙球静置于B处,质量为
的乙球静置于B处,质量为 的甲球从A处沿圆弧切线方向以速度
的甲球从A处沿圆弧切线方向以速度 开始运动,到达B处与乙球发生碰撞,碰撞时间很短可忽略不计,碰撞为弹性碰撞,两小球可视为质点.当乙球刚运动到D处时,两小球发生第二次碰撞.求:
开始运动,到达B处与乙球发生碰撞,碰撞时间很短可忽略不计,碰撞为弹性碰撞,两小球可视为质点.当乙球刚运动到D处时,两小球发生第二次碰撞.求: 
 ;
;