题目内容
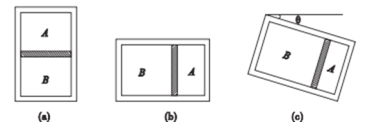
【题目】如图所示，飞行器P绕某星球做匀速圆周运动，下列说法不正确的是（ ）
A.轨道半径越大，周期越长
B.张角越大，速度越大
C.若测得周期和星球相对飞行器的张角，则可得到星球的平均密度
D.若测得周期和轨道半径，则可得到星球的平均密度
【答案】D
【解析】
A．根据开普勒第三定律
，可知轨道半径越大，飞行器的周期越长， A正确；
B．根据卫星的速度公式
，可知张角越大，轨道半径越小，速度越大，B正确；
C．根据公式
可得
设星球的质量为M，半径为R，平均密度为ρ，飞行器的质量为m，轨道半径为r，周期为T，对于飞行器，由几何关系得
星球的平均密度为
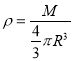
由以上三式知，测得周期和张角，就可得到星球的平均密度，C正确；
D．由可得
星球的平均密度为
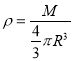
可知若测得周期和轨道半径，可得到星球的质量，但星球的半径未知，不能求出星球的体积，故不能求出平均密度，D错误。
故选D。
练习册系列答案
英才计划期末调研系列答案
相关题目
【题目】木卫一、木卫二和木卫三都在木星的赤道平面内绕木星做匀速圆周运动（公转），部分参数如下表，万有引力常量G=6.67×10-11N·m2/kg2。可推算出（ ）
编号 | 质量/kg | 轨道半径/km | 周期/d |
木卫一 | 4．2×105 | 1．77 | |
木卫二 | 4．8×1022 | 6．7×105 | |
木卫三 | 15×1022 | 7．15 |
A.木卫一的质量B.木卫二的周期
C.木卫三的密度D.木星表面的重力加速度
