题目内容
14. 一长轻质木板置于光滑水平地面上,木板上放着质量分别为mA=1kg和mB=2kg的A、B两物块,A、B与木板之间的动摩擦因数都为μ=0.2,水平恒力F作用在A物块上,如图所示(重力加速g=10m/s2).则( )
一长轻质木板置于光滑水平地面上,木板上放着质量分别为mA=1kg和mB=2kg的A、B两物块,A、B与木板之间的动摩擦因数都为μ=0.2,水平恒力F作用在A物块上,如图所示(重力加速g=10m/s2).则( )| A. | 若F=1N,则物块、木板都静止不动 | |
| B. | 若F=1.5N,则A物块所受摩擦力大小为1.5N | |
| C. | 若F=4N,则B物块所受摩擦力大小为2N | |
| D. | 若F=8N,则B物块的加速度为1.0m/s2 |
分析 根据滑动摩擦力公式求出A、B与木板之间的最大静摩擦力,比较拉力和最大静摩擦力之间的关系判断物体的运动情况,进而判断物体所受摩擦力的情况,根据牛顿第二定律求出B的加速度.
解答 解:A与木板间的最大静摩擦力fA=μmAg=0.2×1×10N=2N,
B与木板间的最大静摩擦力fB=μmBg=0.2×2×10N=4N,
A、F=1N<fA,所以AB与木板保持相对静止,整体在F作用下向左匀加速运动,故A错误;
B、若F=1.5N<fA,所以AB与木板保持相对静止,整体在F作用下向左匀加速运动,根据牛顿第二定律得:F=(mA+mB)a;
解得:a=$\frac{1.5}{1+2}=0.5m/{s}^{2}$;对A来说,则有:F-fA=mAa,解得:fA=1.5-1×0.5=1N;对B来说,则有:fB=ma=2×0.5=1N,故B错误;
C、F=4N>fA,所以A在木板上滑动,B和木板整体受到摩擦力2N,轻质木板,质量不计,所以B的加速度a=$\frac{f}{{m}_{B}}$=$\frac{2}{2}$m/s2=1m/s2
对B进行受力分析,摩擦力提供加速度,f′=mBa=2×1=2N,故C正确;
D、F=8N>fA,所以A相对于木板滑动,B和木板整体受到摩擦力2N,轻质木板,质量不计,所以B的加速度a=$\frac{f}{{m}_{B}}$=$\frac{2}{2}$m/s2=1m/s2,故D正确.
故选:CD.
点评 本题以常见的运动模型为核心,考查了摩擦力、牛顿第二定律、隔离法与整体法的应用等知识;解决的关键是正确对两物体进行受力分析.

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
5.细胞膜也称生物膜或质膜.是由类脂、蛋白质和糖类组成.质膜中的类脂也称膜脂,是质膜的基本骨架,膜蛋白质是膜功能的主要体现者.如果细胞膜的厚度约等于800nm(1nm=10-9 m),当膜的内外层间的电压达到0.4V时,即可让一价钠离子渗透.设细胞膜内的电场为匀强电场,则钠离子在渗透时( )
| A. | 膜内电场强度约为4×105 V/m | |
| B. | 膜内电场强度约为2×105 V/m | |
| C. | 每个钠离子沿电场方向透过膜时电场力做功约为6.4×10-20 J | |
| D. | 每个钠离子沿电场方向透过膜时电场力做功约为1.6×10-19 J |
2.如图是一辆汽车做直线运动的xt图象,对线段OA、AB、BC、CD所表示的运动,下列说法错误的是( )
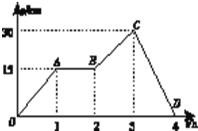

| A. | 4 h内汽车的位移大小为零 | |
| B. | 汽车在AB段静止 | |
| C. | CD段表示汽车的运动方向与初始运动方向相反 | |
| D. | 汽车在OA段运动得最快 |
9.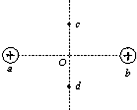 a、b为两个带等量正电荷的固定的小球,O为ab连线的中点,如图所示,c、d为中垂线上的两对称点且离O点很近,若在C点由静止释放一个电子,关于电子的运动,以下叙述不正确的有( )
a、b为两个带等量正电荷的固定的小球,O为ab连线的中点,如图所示,c、d为中垂线上的两对称点且离O点很近,若在C点由静止释放一个电子,关于电子的运动,以下叙述不正确的有( )
 a、b为两个带等量正电荷的固定的小球,O为ab连线的中点,如图所示,c、d为中垂线上的两对称点且离O点很近,若在C点由静止释放一个电子,关于电子的运动,以下叙述不正确的有( )
a、b为两个带等量正电荷的固定的小球,O为ab连线的中点,如图所示,c、d为中垂线上的两对称点且离O点很近,若在C点由静止释放一个电子,关于电子的运动,以下叙述不正确的有( )| A. | 在C→O的过程中,做匀加速运动 | B. | 在C→O的过程中,做变加速运动 | ||
| C. | 在O点速度最大,加速度为零 | D. | 电子在cd间做往复运动 |
19.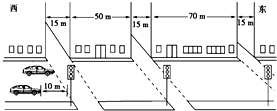 如图所示的交通图,每一个路口都有红绿灯,并且限速50km/h.假设你正从西以最高限速向东行驶,当你距离第一个路口10m时所有的绿灯都亮了.每个绿灯均亮13s.你能够不用刹车顺利穿过所有的路口吗?
如图所示的交通图,每一个路口都有红绿灯,并且限速50km/h.假设你正从西以最高限速向东行驶,当你距离第一个路口10m时所有的绿灯都亮了.每个绿灯均亮13s.你能够不用刹车顺利穿过所有的路口吗?
 如图所示的交通图,每一个路口都有红绿灯,并且限速50km/h.假设你正从西以最高限速向东行驶,当你距离第一个路口10m时所有的绿灯都亮了.每个绿灯均亮13s.你能够不用刹车顺利穿过所有的路口吗?
如图所示的交通图,每一个路口都有红绿灯,并且限速50km/h.假设你正从西以最高限速向东行驶,当你距离第一个路口10m时所有的绿灯都亮了.每个绿灯均亮13s.你能够不用刹车顺利穿过所有的路口吗?
3.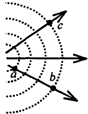 如图所示,实线为电场线,虚线为等势线即等势面与纸面的交线.a、b、c是电场中的三个点,以下说法正确的是( )
如图所示,实线为电场线,虚线为等势线即等势面与纸面的交线.a、b、c是电场中的三个点,以下说法正确的是( )
 如图所示,实线为电场线,虚线为等势线即等势面与纸面的交线.a、b、c是电场中的三个点,以下说法正确的是( )
如图所示,实线为电场线,虚线为等势线即等势面与纸面的交线.a、b、c是电场中的三个点,以下说法正确的是( )| A. | b、c两点的电场强度相同 | |
| B. | a、b两点的电场强度相同 | |
| C. | a、b两点间的电势差等于a、c两点间的电势差 | |
| D. | 将检验电荷从b点移动到c点,电场力做正功 |
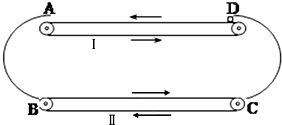 如图所示,以A、B和C、D为端点的半径为R=0.9m的两半圆形光滑轨道固定于竖直平面内,A、D之间放一水平传送带Ⅰ,B、C之间放一水平传送带Ⅱ,传送带Ⅰ以V1=8m/s的速度沿图示方向匀速运动,传送带Ⅱ以V2=10m/s的速度沿图示方向匀速运动.现将质量为m=2kg的物块从传送带Ⅰ的右端由静止放上传送带,物块运动第一次到A时恰好能沿半圆轨道滑下.物块与传送带Ⅱ间的动摩擦因数为μ2=0.35,不计物块的大小及传送带与半圆轨道间的间隙,重力加速度g=10m/s2,已知A、D端之间的距离为L=1.0m.求:
如图所示,以A、B和C、D为端点的半径为R=0.9m的两半圆形光滑轨道固定于竖直平面内,A、D之间放一水平传送带Ⅰ,B、C之间放一水平传送带Ⅱ,传送带Ⅰ以V1=8m/s的速度沿图示方向匀速运动,传送带Ⅱ以V2=10m/s的速度沿图示方向匀速运动.现将质量为m=2kg的物块从传送带Ⅰ的右端由静止放上传送带,物块运动第一次到A时恰好能沿半圆轨道滑下.物块与传送带Ⅱ间的动摩擦因数为μ2=0.35,不计物块的大小及传送带与半圆轨道间的间隙,重力加速度g=10m/s2,已知A、D端之间的距离为L=1.0m.求: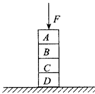 如图所示,水平面上,四个木块A、B、C、D叠放在一起,处于静止状态.现用一竖直向下的力F作用于木块A上,则木块D所受力的个数为( )
如图所示,水平面上,四个木块A、B、C、D叠放在一起,处于静止状态.现用一竖直向下的力F作用于木块A上,则木块D所受力的个数为( )