题目内容
单色细光束射到折射率n=  的透明球表面,光束在过球心的平面内,入射角θ1=45°,研究经折射进入球内后又经内表面反射一次,再经球面折射后射出的光线,如图所示(图上已画出入射光线和出射光线).
的透明球表面,光束在过球心的平面内,入射角θ1=45°,研究经折射进入球内后又经内表面反射一次,再经球面折射后射出的光线,如图所示(图上已画出入射光线和出射光线).
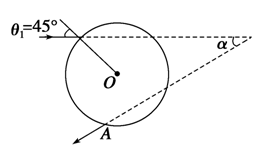
(1)在图上大致画出光线在球内的路径和方向;
(2)求入射光线与出射光线之间的夹角α;
 的透明球表面,光束在过球心的平面内,入射角θ1=45°,研究经折射进入球内后又经内表面反射一次,再经球面折射后射出的光线,如图所示(图上已画出入射光线和出射光线).
的透明球表面,光束在过球心的平面内,入射角θ1=45°,研究经折射进入球内后又经内表面反射一次,再经球面折射后射出的光线,如图所示(图上已画出入射光线和出射光线).
(1)在图上大致画出光线在球内的路径和方向;
(2)求入射光线与出射光线之间的夹角α;
(1)
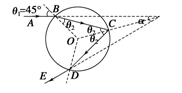
(2) α=30°.

(2) α=30°.
(1)光线在球内的路径和方向如下图所示.

(2)由折射定律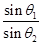 =n.
=n.
得sin θ2=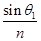 =
=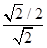 =
=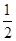 ,所以θ2=30°
,所以θ2=30°
由几何关系及对称性,有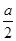 =θ2-(θ1-θ2)=2θ2-θ1,
=θ2-(θ1-θ2)=2θ2-θ1,
α=4θ2-2θ1把θ2=30°,θ1=45°代入,得α=30°.
本题考查光的折射定律,光路图如图所示,根据公式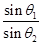 =n.,可算出折射角,然后根据几何对称性,可得入射光线和射出光线的夹角。
=n.,可算出折射角,然后根据几何对称性,可得入射光线和射出光线的夹角。

(2)由折射定律
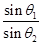 =n.
=n.得sin θ2=
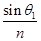 =
=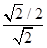 =
=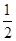 ,所以θ2=30°
,所以θ2=30°由几何关系及对称性,有
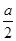 =θ2-(θ1-θ2)=2θ2-θ1,
=θ2-(θ1-θ2)=2θ2-θ1,α=4θ2-2θ1把θ2=30°,θ1=45°代入,得α=30°.
本题考查光的折射定律,光路图如图所示,根据公式
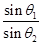 =n.,可算出折射角,然后根据几何对称性,可得入射光线和射出光线的夹角。
=n.,可算出折射角,然后根据几何对称性,可得入射光线和射出光线的夹角。
练习册系列答案
相关题目

 为直角。此截面所在平面内的光线沿平行于BC边的方向射到AB边,进入棱镜后直接射到AC边上,并刚好能发生全反射。该棱镜材料的折射率为 ( )
为直角。此截面所在平面内的光线沿平行于BC边的方向射到AB边,进入棱镜后直接射到AC边上,并刚好能发生全反射。该棱镜材料的折射率为 ( )




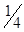 透明圆柱体放在水平面上,AOB为
透明圆柱体放在水平面上,AOB为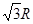 ,则:
,则: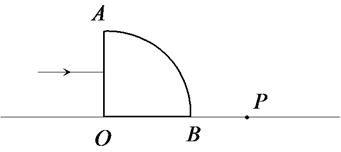

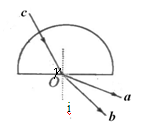
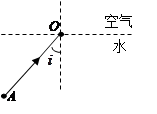

 不变而逐渐增大入射角,则关于红光和紫光的下述说法中正确的是
不变而逐渐增大入射角,则关于红光和紫光的下述说法中正确的是
 点,则紫光在
点,则紫光在