Question

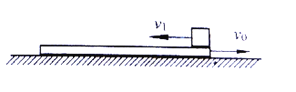
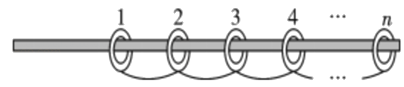
【题目】如图，某根水平固定的长木杆上有n（n≥3）个质量均为m的圆环（内径略大于木杆直径），每相邻的两个圆环之间有不可伸长的柔软轻质细线相连，细线长度均为L，开始时所有圆环挨在一起（但未相互挤压）；现给第1个圆环一个初速度使其在木杆上向左滑行，当前、后圆环之间的细线拉紧后都以共同的速度向前滑行，但第n个圆环恰好未被拉动。已知所有细线拉紧的时间极短，且每个圆环与木杆间的动摩擦因数均为μ，求

（1）当n＝3时，整个运动过程中克服摩擦力做的功；

（2）当n＝3时，求第一个圆环向左运动的初速度大小v；

（3）若第一个圆环的初速度大小为v0，求整个过程中由于细绳拉紧损失的机械能。

Answer 1

【答案】（1）；（2）（3）

【解析】

（1）当n＝3时，仅有1、2两个圆环在运动，克服摩擦力做的功为：

Wf＝μmgL+μmg2L＝3μmgL…①

（2）当n＝3时，易知从1开始运动到2、3之间的细绳恰好拉直的过程中，有：

…②

1、2之间的细绳拉直过程，取向左为正方向，由动量守恒有 mv1＝2mv2…③

＝μ2mgL…④

由以上三式可得 v＝…⑤

（3）从开始运动到第n个圆环恰好被拉动的过程中，克服摩擦力做功为：

Wf′＝μmgL+μmg2L+μmg（n﹣1）L＝ μmgL…⑥

由能量守恒可知

…⑦