题目内容
【题目】如图所示,两平行光滑金属导轨由两部分组成,左面部分水平,右面部分为半径r=0.5m的竖直半圆,两导轨间距离d=0.3m,导轨水平部分处于竖直向上、磁感应强度大小B=1T的匀强磁场中,两导轨电阻不计。有两根长度均为d的金属棒ab、cd,均垂直导轨置于水平导轨上,金属棒ab、cd的质量分别为m1=0.2kg、m2=0.1kg,电阻分别为R1=0.1Ω、R2=0.2Ω。现让ab棒以v0=10m/s的初速度开始水平向右运动,cd棒进入圆轨道后,恰好能通过轨道最高点PP′,cd棒进入圆轨道前两棒未相碰,重力加速度g=10m/s2,求:
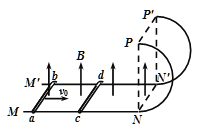
(1)ab棒开始向右运动时cd棒的加速度a0;
(2)cd棒刚进入半圆轨道时ab棒的速度大小v1;
(3)cd棒进入半圆轨道前ab棒克服安培力做的功W.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】(1)ab棒开始向右运动时,设回路电流为I,有
E=Bdv0
![]()
BId=m2a0
解得:a0=30m/s2
(2)设cd棒刚进入圆形轨道时的速度为v2,有m1v0=m1v1+m2v2
![]()
![]()
解得:v1=7.5m/s
(3)![]()
解得:W=4.375J

练习册系列答案
相关题目