Question

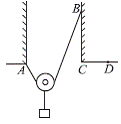
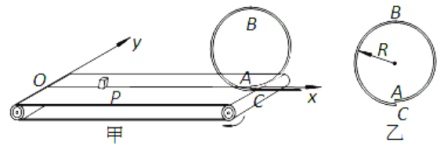
【题目】如图甲所示，水平传送带以 5．0m/s 恒定的速率运转，两皮带轮之间的距 离 l=6m，皮带轮的半径大小可忽略不计。沿水平传送带的上表面建立 xOy 坐标系，坐标 原点 O 在传送带的最左端。半径为 R 的光滑圆轨道 ABC 的最低点 A 点与 C 点原来相连， 位于竖直平面内（如图乙所示），现把它从最低点处切开，并使 C 端沿 y 轴负方向错开少 许，把它置于水平传送带的最右端， A 点位于 x 轴上且与传送带的最右端之间的距离可忽 略不计，轨道的 A、 C 两端均位于最低点， C 端与一水平直轨道平滑连接。 由于 A、 C 两 点间沿 y 轴方向错开的距离很小，可把 ABC 仍看作位于竖直平面内的圆轨道。将一质量m=1kg 的小物块 P（可视为质点）沿 x 轴轻放在传送带上某处，小物块随传送带运动到 A 点进入光滑圆轨道，恰好能够通过圆轨道的最高点B，并沿竖直圆轨道 ABC 做完整的圆周运动后由 C 点经水平直轨道滑出。已知小物块与传送带间的动摩擦因数 μ=0．5，圆轨道 的半径 R=0．5m，取重力加速度 g=10m/s2。求：

（1）物块通过圆轨道最低点 A 时对轨道压力的大小；

（2）轻放小物块位置的 x 坐标应满足什么条件，才能完成上述运动；

（3）传送带由电动机带动，其与轮子间无相对滑动，不计轮轴处的摩擦。若将小物 块轻放在传送带上 O 点，求将小物块从 O 点运送至 A 点过程中电动机多做的功。

Answer 1

【答案】（1）60N；（2）x≤3．5m；（3）25J

【解析】

试题分析：1）设物块恰好通过圆轨道最高点B时的速率为vB，根据牛顿第二定律有：

解得：

设物块通过圆轨道最低点A的速率为vA，对于物块由A点运动至B点的过程，根据机械能守恒定律有：

mvA2=m vB2+2mgR

代入数据解得：vA=5．0m/s

设物块通过圆轨道最低点A时，轨道对物块的支持力为FN，根据牛顿第二定律有：；

代入数据解得：FN=60N

据牛顿第三定律，物块通过圆轨道最低点A对轨道的压力为：F′N=FN=60N

（2）物块在传送带上的加速度为：a=μg=5．0m/s2

根据（1）可知物块运动至A点的速度满足vA=5．0m/s，

可使其恰好通过圆轨道最高点B．传送带的速率为：v0=5．0m/s，

物块在传送带上加速运动的位移为：，

故轻放小物块的位置坐标需满足：x≤l-x0=3．5m

（3）设为将小物块从O点运送到A点传送带电动机做的功为W，小物块加速运动时间为：，

小物块加速运动的位移：x=at2=2．5m

根据功能关系有：W=mvA2+μmg（v0t-x）=25J