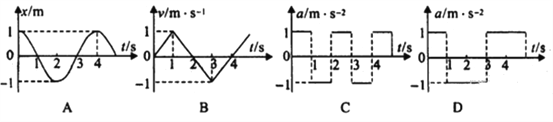
��Ŀ����
����Ŀ����ͼ��ʾ�����������30���Ĺ⻬б���������������ʵ��������ӵ����A��B�����ǵ�������Ϊm�����ɵľ���ϵ��Ϊk��CΪһ�̶����壬ϵͳ���ھ�ֹ״̬���ֿ�ʼ��һ��б�淽�����F�����Aʹ֮�����ȼ����˶��������B��Ҫ�뿪CʱF�Ĵ�СǡΪ2mg���ʣ�

(1)��F��ʼ���õ����B��Ҫ�뿪C�Ĺ����е��ɵ��������A���Ĺ���
(2)���B��Ҫ�뿪Cʱ���A�Ķ��ܣ�
(3)��F��ʼ���õ����B��Ҫ�뿪C�Ĺ�������F���Ĺ���
���𰸡���1��0��2��![]() ��3��
��3��![]()
����������1����2����x1��ʾδ��Fʱ���ɵ�ѹ�������ɺ��˶��ɺ�ţ�ٶ��ɿ�֪��
mgsin30��=kx1
��x2��ʾB ��Ҫ�뿪Cʱ���ɵ��쳤����a��ʾ��ʱA �ļ��ٶȣ��ɺ��˶��ɺ�ţ�ٶ��ɿ�֪��
kx2=mgsin30��
F-mgsin30��-kx2=ma
��F=2mg����=30���������ϸ�ʽ����ã�a=g
��x1+x2=![]() at2
at2
��ã�![]()
���B��Ҫ�뿪Cʱ�����A���ٶ�Ϊ��v=at=g![]()
�ʶ���Ϊ��![]()
��ʱ���ɵ��쳤����F��ʼ����ʱ��ѹ������ͬ�����ɵĵ������ܸı���Ϊ�㣬�ʵ��ɵ�������Ϊ�㣻
��3���ɶ��ܶ����ã�
WF-mg��x1+x2��sin30��=![]() mv2
mv2
��ã�![]()

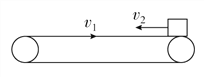
����Ŀ��ijͬѧ��������װ�ö����ʵ��ɵĵ������ܽ���̽����һ���ʵ��ɷ����ڹ⻬ˮƽ�����ϣ�������˹̶����Ҷ���һС��Ӵ��������������ɴ���ԭ��ʱ��С��ǡ���������Ե����ͼ��a����ʾ��������С��ʹ����ѹ��һ�ξ�����ɾ�ֹ�ͷţ�С���뿪������䵽ˮƽ���森ͨ�������ͼ��㣬����õ��ɱ�ѹ����ĵ������ܣ��ش��������⣺
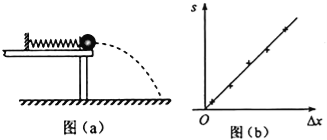
��1����ʵ���п���Ϊ�����ɱ�ѹ����ĵ�������Ep��С���׳�ʱ�Ķ���Ek��ȣ���֪�������ٶȴ�СΪg��Ϊ���Ek��������Ҫ���������������е� ������ȷ�𰸱�ţ���
A���������m |
B��С���׳��㵽��ص��ˮƽ����s |
C�����浽����ĸ߶�h |
D�����ɵ�ѹ������x |
E������ԭ��l0
��2������ѡȡ�IJ���������֪����ʾEk����Ek= ��
��3��ͼ��b���е�ֱ����ʵ������õ���s����xͼ�ߣ��������Ͽ��Ƴ������h���䣮m���ӣ�s����xͼ�ߵ�б�ʻ� ������������������С�������������������m���䣬h���ӣ�s����xͼ�ߵ�б�ʻ� ������������������С������������������ͼ��b�� �и�����ֱ�߹�ϵ��Ek�ı���ʽ��֪��Ep����x�� �η������ȣ�