题目内容
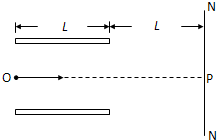
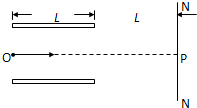
如图所示,水平放置的两块平行金属板,两板间存在竖直向下的匀强电场和垂直纸面的匀强磁场,磁感应强度为B.一质量为m、带电量为+q的微粒以一定的水平初速度从两极板中轴线OP射入板间,它受到的洛伦兹力是电场力的2倍,并恰好做直线运动.现将匀强磁场撤去,使该微粒以相同的水平初速度仍从两极板中轴线OP射入板间,飞出板后,继续运动,打在屏NN′上的S点(未标出).已知金属板长L,屏与金属板右端距离也是L.求:
(1)匀强磁场的方向;
(2)微粒的水平初速度多大?
(3)S点到中轴线OP的距离PS(P点在屏上).
(1)匀强磁场的方向;
(2)微粒的水平初速度多大?
(3)S点到中轴线OP的距离PS(P点在屏上).

(1)粒子恰好做直线运动,可知粒子受电场力、重力与洛仑兹力平衡,
受到的洛伦兹力是电场力的2倍,电场力方向向下,所以洛伦兹力方向向上,
根据左手定则得匀强磁场的方向是垂直纸面向里.
(2)粒子受电场力、重力与洛仑兹力平衡,根据平衡条件得:
mg+F电=F洛
F洛=Bqυ
F洛=2F电
解得:υ=
;
(3)根据F洛=2F电和mg+F电=F洛得
F电=mg
粒子在水平方向做匀速直线运动,
υt=L
竖直方向做加速度是2g的匀加速直线运动,
y1=
(g+
)t2=gt2
υy=(g+
)t=2gt
出电场区域后,粒子在竖直方向做加速度是g的匀加速直线运动,
y2=υyt+
gt2
所以S点到中轴线OP的距离h=y1+y2=
B2q2L2;
答:(1)匀强磁场的方向是垂直纸面向里;
(2)微粒的水平初速度是
(3)S点到中轴线OP的距离是
B2q2L2.
受到的洛伦兹力是电场力的2倍,电场力方向向下,所以洛伦兹力方向向上,
根据左手定则得匀强磁场的方向是垂直纸面向里.
(2)粒子受电场力、重力与洛仑兹力平衡,根据平衡条件得:
mg+F电=F洛
F洛=Bqυ
F洛=2F电
解得:υ=
| 2mg |
| Bq |
(3)根据F洛=2F电和mg+F电=F洛得
F电=mg
粒子在水平方向做匀速直线运动,
υt=L
竖直方向做加速度是2g的匀加速直线运动,
y1=
| 1 |
| 2 |
| F电 |
| m |
υy=(g+
| F电 |
| m |
出电场区域后,粒子在竖直方向做加速度是g的匀加速直线运动,
y2=υyt+
| 1 |
| 2 |
所以S点到中轴线OP的距离h=y1+y2=
| 7 |
| 8m2g |
答:(1)匀强磁场的方向是垂直纸面向里;
(2)微粒的水平初速度是
| 2mg |
| Bq |
(3)S点到中轴线OP的距离是
| 7 |
| 8m2g |


练习册系列答案
相关题目
















