题目内容
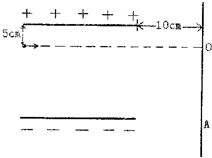
 一质量m=5×10-3kg(忽略重力)的微粒带正电、电量q=1×10-4C.从距上极板15cm处以v0=2m/s的水平初速度,进入长l1=20cm板间距d=30cm的两极板间,如果两极板不带电,微粒将运动到距极板最右端l2=10cm的竖直荧光屏上的o点.现将两极板间加U=300V的电压,带电微粒打到荧光屏上的A点.
一质量m=5×10-3kg(忽略重力)的微粒带正电、电量q=1×10-4C.从距上极板15cm处以v0=2m/s的水平初速度,进入长l1=20cm板间距d=30cm的两极板间,如果两极板不带电,微粒将运动到距极板最右端l2=10cm的竖直荧光屏上的o点.现将两极板间加U=300V的电压,带电微粒打到荧光屏上的A点.(1)OA两点的间距为多少?
(2)带电微粒进入电场到打到荧光屏上的A点过程中电场力对其做功多少?
分析:(1)运动具有独立性,带电微粒在水平方向上不受力做匀速直线运动,由t=
可求时间;0A间的距离为偏转位移y1+匀速运动的分位移y2,可由直角三角形求出y2
(2)带电粒子在电场中偏转时,电场力做功W=F?y.
| x |
| v |
(2)带电粒子在电场中偏转时,电场力做功W=F?y.
解答:解:(1)由运动的独立性,带电微粒在水平方向上不受力做匀速直线运动,
由t=
得粒子在电场中运动的时间:t1=
=
s=0.1s
粒子受到的电场力:F=qE=
=0.1N
粒子的加速度:a=
=
m/s2=20m/s2
偏转位移:y1=
a
=
×20×0.12m=0.1m
速度偏转角:tanα=
=
=
=1
粒子离开电场后做匀速直线运动,由直角三角形,则y2=l2?tanα=0.1tanα=0.1×1=0.1m
OA间的距离为:y1+y2=0.1+0.1=0.2m
(2)带电粒子在电场中偏转时,电场力做功:W=F?y1=0.1×0.1J=0.01J
答:(1)OA两点的间距为0.2m; (2)带电微粒进入电场到打到荧光屏上的A点过程中电场力对其做功W=0.01J.
由t=
| x |
| v |
| l1 |
| v0 |
| 0.2 |
| 2 |
粒子受到的电场力:F=qE=
| qU |
| d |
粒子的加速度:a=
| F |
| m |
| 0.1 |
| 5×10-3 |
偏转位移:y1=
| 1 |
| 2 |
| t | 2 1 |
| 1 |
| 2 |
速度偏转角:tanα=
| vy |
| vx |
| at1 |
| v0 |
| 20×0.1 |
| 2 |
粒子离开电场后做匀速直线运动,由直角三角形,则y2=l2?tanα=0.1tanα=0.1×1=0.1m
OA间的距离为:y1+y2=0.1+0.1=0.2m
(2)带电粒子在电场中偏转时,电场力做功:W=F?y1=0.1×0.1J=0.01J
答:(1)OA两点的间距为0.2m; (2)带电微粒进入电场到打到荧光屏上的A点过程中电场力对其做功W=0.01J.
点评:该题的情景类似于示波器的原理,考查了类平抛运动,理解运动的合成与分解,运动的独立性、等是性.属于中档题目.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
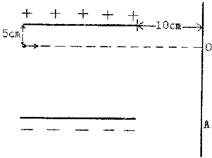 一质量m=5×10-3kg(忽略重力)的微粒带正电、电量q=1×10-4C.从距上极板5cm处以2m/s的水平初速度,进入长为20cm板间距也为20cm的两极板间,如果两极板不带电,微粒将运动到距极板最右端10cm的竖直荧光屏上的O点.现将两极板间加200V的电压,带电微粒打到荧光屏上的A点.
一质量m=5×10-3kg(忽略重力)的微粒带正电、电量q=1×10-4C.从距上极板5cm处以2m/s的水平初速度,进入长为20cm板间距也为20cm的两极板间,如果两极板不带电,微粒将运动到距极板最右端10cm的竖直荧光屏上的O点.现将两极板间加200V的电压,带电微粒打到荧光屏上的A点.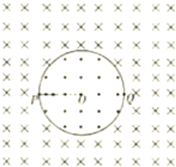 如图所示,在真空中半径为
如图所示,在真空中半径为