Question

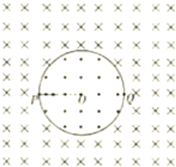如图所示，在真空中半径为R=

3

m的圆形磁场区域里加上垂直于纸面向外的磁感应强度为B₁=1T的匀强磁场，在圆形磁场区域外加上与B₁方向相反的匀强磁场B₂，P、Q是圆周上过直径的两个点，从P点沿半径方向以v=1×10⁴m/s射入一质量m=5×10^-10kg，电荷 量q=5×10^-6C的带电粒子，不计重力作用．
求：
（1）若要使该粒子从P出发，经B₁、B₂磁场，第一次从Q点沿半径方向射入圆形磁场区域，则所需磁场B₂．
（2）粒子从P点射入后第一次回到P点经过的时间．

Answer 1

分析：（1）若要使该粒子从P出发，经B₁、B₂磁场，第一次从Q点沿半径方向射入圆形磁场区域，根据几何关系求出粒子在磁场B₂区域内的半径，根据半径公式求出磁场B₂的大小．
（2）根据几何关系分别求出粒子在两个磁场中运动圆弧的圆心角大小，结合周期公式求出运动的时间．

解答：解：（1）带电粒子在圆形磁场中做圆周运动的半径为r₁，圆心为O₁．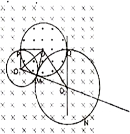
qvB=m

v2

r1

．
r1=

mv

qB

=

5×10-10×1×104

5×10-6×1

=1m
tan∠POO1=

r1

R

=

1

3

则∠POO₁=30°
粒子从M点离开磁场区域B₁进入磁场区域B₂．
在B₂磁场中做圆周运动的半径为r₂，圆心为O₂，由几何关系得，∠MOO₂=60°
r₂=Rcot30°=3m
B2=

mv

qr2

=

5×10-10×1×104

5×10-6×3

=0.33T
（2）粒子在B₁磁场中运动的周期为T₁．
T1=

2πm

qB1

=2π×10-4s．
从P点沿圆弧PM运动到M点的时间为t₁．
t1=

120°

360°

T1=

2π

3

×10-4s
粒子在B₂磁场中运动的周期为T₂．
T2=

2πm

qB2

=

2π

3

×10-4s
粒子从M点进入B₂磁场运动到Q点所用的时间为t₂，转过的圆心角为300°．
t2=

300

360

T2=

5π

9

×10-4s
根据对称性从Q点进入B₁磁场运动到P点所用的时间为t₁+t₂．
粒子从P点射出，第一次回到P所用的时间为t．
t=2(t1+t2)=

22π

9

×10-4s．
答：（1）所需磁场B₂为0.33T．
（2）粒子从P点射入后第一次回到P点经过的时间为

22π

9

×10-4s．

点评：解决本题的关键掌握带电粒子在磁场中运动的半径公式和周期公式，本题对数学几何能力要求较高，需加强训练．