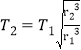Question

【题目】（20分）如图所示，装置的左边是足够长的光滑水平面，一轻质弹簧左端固定，右端连接着质量 M=2kg的小物块A。装置的中间是水平传送带，它与左右两边的台面等高，并能平滑对接。传送带始终以u="2m/s" 的速率逆时针转动。装置的右边是一光滑的曲面，质量m=1kg的小物块B从其上距水平台面h=1.0m处由静止释放。已知物块B与传送带之间的摩擦因数μ=0.2，l=1.0m。设物块A、B中间发生的是对心弹性碰撞，第一次碰撞前物块A静止且处于平衡状态。取g=10m/s2。

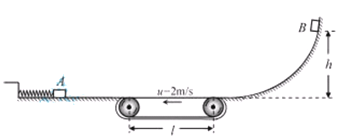
（1）求物块B与物块A第一次碰撞前速度大小；

（2）通过计算说明物块B与物块A第一次碰撞后能否运动到右边曲面上？

（3）如果物块A、B每次碰撞后，物块A再回到平衡位置时都会立即被锁定，而当他们再次碰撞前锁定被解除，试求出物块B第n次碰撞后的运动速度大小。

Answer 1

【答案】（1）4m/s （2）不能 （3）

【解析】

（1）设物块B沿光滑曲面下滑到水平位置时的速度大小为v0

由机械能守恒知

①

②

设物块B在传送带上滑动过程中因受摩擦力所产生的加速度大小为a

③

设物块B通过传送带后运动速度大小为v，有

④

结合②③④式解得

v=4m/s ⑤

由于=2m/s，所以v=4m/s即为物块B与物块A第一次碰撞前的速度大小

（2）设物块A、B第一次碰撞后的速度分别为V、v1，取向右为正方向，由弹性碰撞知

⑥

⑦

解得⑧

即碰撞后物块B沿水平台面向右匀速运动

设物块B在传送带上向右运动的最大位移为，则

⑨

⑩

所以物块B不能通过传送带运动到右边的曲面上

（3）当物块B在传送带上向右运动的速度为零时，将会沿传送带向左加速。可以判断，物块B运动到左边台面是的速度大小为v1，继而与物块A发生第二次碰撞。设第二次碰撞后物块B速度大小为v2，同上计算可知

11

物块B与物块A第三次碰撞、第四次碰撞……，碰撞后物块B的速度大小依次为

…… 12

则第n次碰撞后物块B的速度大小为

13

14