题目内容
14. 如图所示,底边长为2L,θ=30°的等腰三角形区域内(O为底边中点)有垂直纸面向外的匀强磁场.现有一质量为m,电量为q的带正电粒子从静止开始经过电势差为U的电场加速后,从O点垂直于AB进入磁场,不计粒子重力与空气阻力的影响,不计粒子与AB板碰撞的作用时间,设粒子与AB板碰撞前后,电量保持不变并以相同的速率反弹.求:
如图所示,底边长为2L,θ=30°的等腰三角形区域内(O为底边中点)有垂直纸面向外的匀强磁场.现有一质量为m,电量为q的带正电粒子从静止开始经过电势差为U的电场加速后,从O点垂直于AB进入磁场,不计粒子重力与空气阻力的影响,不计粒子与AB板碰撞的作用时间,设粒子与AB板碰撞前后,电量保持不变并以相同的速率反弹.求:(1)粒子经电场加速射入磁场时的速度;
(2)磁感应强度B为多少时,粒子能以最大的圆周半径偏转后打到AB板;
(3)如果粒子经AB板碰撞一次后,以垂直于AC速度射出磁场,求粒子在磁场中运动的时间;
(4)粒子在磁场中的运动时间随着磁感应强度的增大而增加,求粒子在磁场内运动的极限时间.
分析 (1)根据动能定理求出粒子经电场加速后射入磁场时的速度.
(2)要使圆周半径最大,则粒子的圆周轨迹应与AC边相切,作出粒子的运动轨迹,根据几何关系求出半径,结合半径公式求出磁感应强度的大小.
(3)作出粒子的运动轨迹,根据弧长和速度求出运动的时间.
(4)当r越小,后一次打到ED板的点越靠近E端点,在磁场中圆周运动累积路程越大,时间越长.当r为无穷小,经过n个半圆运动,最后一次打到E点.
解答 解:(1)依题意,粒子经电场加速射入磁场时的速度为v,由动能定理得: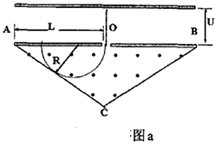
由$qU=\frac{1}{2}m{v}^{2}$,①
得v=$\sqrt{\frac{2qU}{m}}$. ②
(2)要使圆周半径最大,则粒子的圆周轨迹应与AC边相切,设圆周半径为R,
由图中几何关系:R+$\frac{R}{sinθ}$=L ③
由洛伦兹力提供向心力:$qvB=m\frac{{v}^{2}}{R}$ ④
联立①②③④解得B=$\frac{3\sqrt{2Uqm}}{qL}$. ⑤
(3)由图b可知,运动的半径r=$\frac{L}{3}$,
${t}_{1}=\frac{πL}{3v}$,
${t}_{2}=\frac{\frac{π}{6}}{2π}•\frac{2πL}{3v}=\frac{πL}{18v}$.
则$t={t}_{1}+{t}_{2}=\frac{7πL}{18v}$=$\frac{7πL}{18}\sqrt{\frac{m}{2qU}}$.
(4)如图c,设粒子运动圆周半径为r,则r=$\frac{mv}{qB}$,
当r越小,最后一次打到AB板的点越靠近A端点,在磁场中圆周运动累积路程越大,时间越长,当r为无穷小,经过n个半圆圆周运动,如图所示,最后一次打到A点.
有:$n=\frac{L}{2r}$ ⑥
最长的极限时间${t}_{m}=n\frac{πr}{v}=\frac{πL}{2}\sqrt{\frac{m}{2qU}}$.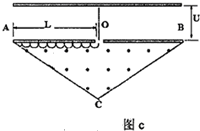
答:(1)粒子经电场加速射入磁场时的速度为$\sqrt{\frac{2qU}{m}}$.
(2)磁感应强度B为$\frac{3\sqrt{2Uqm}}{qL}$时,粒子能以最大的圆周半径偏转后打到AB板.
(3)粒子在磁场中运动的时间为$\frac{7πL}{18}\sqrt{\frac{m}{2qU}}$.
(4)粒子在磁场内运动的极限时间为$\frac{πL}{2}\sqrt{\frac{m}{2qU}}$.
点评 做好此类题目的关键是准确的画出粒子运动的轨迹图,利用几何知识求出粒子运动的半径,再结合半径公式和周期公式去分析.

 某综艺节目,选手表演失败后就从舞台上掉下去,为了安全,人掉在一质量忽略的弹簧垫上,假如掉下落在垫子上可简化为如图所示的运动模型:从O点自由下落,至a点落到弹簧垫上,经过合力为零的b点(虚线位置)到达最低点c(实线位置),然后弹起.整个过程中忽略空气阻力,分析这一过程,下列表述正确的是( )
某综艺节目,选手表演失败后就从舞台上掉下去,为了安全,人掉在一质量忽略的弹簧垫上,假如掉下落在垫子上可简化为如图所示的运动模型:从O点自由下落,至a点落到弹簧垫上,经过合力为零的b点(虚线位置)到达最低点c(实线位置),然后弹起.整个过程中忽略空气阻力,分析这一过程,下列表述正确的是( )| A. | 经过b点时,选手的速率最大 | |
| B. | 从a点到c点,选手的机械能守恒 | |
| C. | 由题可知ac的长度是ab长度的2倍 | |
| D. | 从a点下落到c点过程中,选手的动能和重力势能之和一直减小 |
| A. | 玻尔理论可以成功解释氢原子的光谱现象 | |
| B. | 氢原子的核外电子从半径较小的轨道跃迁到半径较大的轨道时,原子的能量增大 | |
| C. | α粒子散射实验揭示了原子核有复杂结构 | |
| D. | 查德威克发现了中子,其核反应方程为:${\;}_{4}^{9}$Be+${\;}_{2}^{4}$He→${\;}_{6}^{12}$C+${\;}_{0}^{1}$n | |
| E. | 升高或者降低放射性物质的温度均可改变其半衰期 |
 如图所示,现有一带负电荷的粒子能够在相互垂直的匀强电场和匀强磁场中匀速直线穿过.设两极板间电压为U,距离为d,匀强磁场的磁感应强度为B,粒子带电荷量为q,进入速度为v(不及粒子的重力).以下说法正确的是( )
如图所示,现有一带负电荷的粒子能够在相互垂直的匀强电场和匀强磁场中匀速直线穿过.设两极板间电压为U,距离为d,匀强磁场的磁感应强度为B,粒子带电荷量为q,进入速度为v(不及粒子的重力).以下说法正确的是( )| A. | 若同时增大U和B,其他条件不变,则粒子一定能够直线穿过 | |
| B. | 若同时减小d和增大v,其他条件不变,则粒子可能直线穿过 | |
| C. | 若下极板往向下移,则粒子向下偏,动能增加 | |
| D. | 若下极板往下移,则粒子的运动轨迹为抛物线 |
 如图,a、b都是很轻的铝环,环a是闭合的,环b是不闭合的,a、b环都固定在一根可以绕O点自由转动的水平细杆上,此时整个装置静止,下列说法中正确的是( )
如图,a、b都是很轻的铝环,环a是闭合的,环b是不闭合的,a、b环都固定在一根可以绕O点自由转动的水平细杆上,此时整个装置静止,下列说法中正确的是( )| A. | 使条形磁铁N极垂直a环靠近a,a靠近磁铁 | |
| B. | 使条形磁铁N极垂直a环远离a,a靠近磁铁 | |
| C. | 使条形磁铁N极垂直b环靠近b,b靠近磁铁 | |
| D. | 使条形磁铁N极垂直b环靠近b,b远离磁铁 |
| A. | 小船过河的最短时间为24s | B. | 小船过河的最短时间为30s | ||
| C. | 过河的最短位移为150m | D. | 过河的最短位移为120m |
| A. | 3S | B. | 5S | C. | 7S | D. | 9S |
 如图所示v-t图象,表示质点做匀减速直线运动,它的初速度是20m/s,加速度是$-\frac{2}{3}$m/s2.?
如图所示v-t图象,表示质点做匀减速直线运动,它的初速度是20m/s,加速度是$-\frac{2}{3}$m/s2.? 如图所示,在高1.25m的水平桌面上放一个质量为0.5kg的木块,质量为0.1kg的橡皮泥以30m/s的水平速度粘到木块上(粘合过程时间极短).木块在桌面上滑行1.5m后离开桌子落到离桌边2m 的地方.求木块与桌面间的动摩擦因数.(g取10m/s2)
如图所示,在高1.25m的水平桌面上放一个质量为0.5kg的木块,质量为0.1kg的橡皮泥以30m/s的水平速度粘到木块上(粘合过程时间极短).木块在桌面上滑行1.5m后离开桌子落到离桌边2m 的地方.求木块与桌面间的动摩擦因数.(g取10m/s2)