题目内容
(19分)
如图所示,两块很薄的金属板之间用金属杆固定起来使其平行正对,两个金属板完全相同、且竖直放置,金属杆粗细均匀、且处于水平状态。已知两个金属板所组成的电容器的电容为C,两个金属板之间的间距为d,两个金属板和金属杆的总质量为m。整个空间存在一个水平向里的匀强磁场,匀强磁场的磁感应强度为B,磁场方向垂直金属杆,且和金属板平行。现在使整个装置从静止开始在该磁场中释放。重力加速度大小为g。试通过定量计算判断,该装置在磁场中竖直向下做什么运动?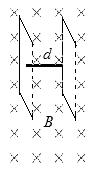
装置在磁场中以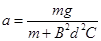 做匀加速直线运动
做匀加速直线运动
解析试题分析:由题意知:导体棒切割磁感线产生感应电动势,装置下落时,两个金属板分别积聚正、负电荷成为一只带电的平行板电容器,等效为导体棒有感应电流产生,受到安培力的作用,由牛顿第二定律列方程可求解加速度。
设经过时间t时,下落速度为v,电容器的带电荷量为Q,电容器两板之间的电压为U,金属杆切割磁感线产生的感生电动势为E,有:
C=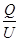 ① (2分)
① (2分)
E=Bdv ② (2分)
U=E ③ (1分)
解得:Q= CBdv ④ (1分)
设在时间间隔(t,t+△t)内流经金属棒的电荷量为△Q,金属棒受到的安培力为F,有:
F=Bid ⑤ (2分)
i=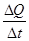 ⑥ (2分)
⑥ (2分)
△Q也是平行板电容器在时间间隔(t,t+△t)内增加的电荷量,由④式得:
△Q= CBd△v ⑦ (2分)
△v为金属棒的速度变化量,有:
a=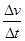 ⑧ (2分)
⑧ (2分)
对金属棒,有:
mg-F=ma ⑨ (2分)
以上联合求解得: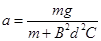 ⑩ (2分)
⑩ (2分)
因为加速度a为常数,所以该装置在磁场中做匀加速直线运动 (1分)
考点:电容 牛顿第二定律 感应电动势

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
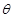 =37o,传送带AB长度xo=l0m。有一水平平台CD高度保持6.45m不变。现调整D端位置,当D、B的水平距离合适时,自D端水平抛出的物体恰好从B点沿BA方向冲上斜面,此后D端固定不动,g=l0m/s2。另外,传送带B端上方安装一极短的小平面,与传送带AB平行共面,保证自下而上传送的物体能沿AB方向由B点斜向上抛出。(sin37o=0.6,cos37o=0.8)
=37o,传送带AB长度xo=l0m。有一水平平台CD高度保持6.45m不变。现调整D端位置,当D、B的水平距离合适时,自D端水平抛出的物体恰好从B点沿BA方向冲上斜面,此后D端固定不动,g=l0m/s2。另外,传送带B端上方安装一极短的小平面,与传送带AB平行共面,保证自下而上传送的物体能沿AB方向由B点斜向上抛出。(sin37o=0.6,cos37o=0.8)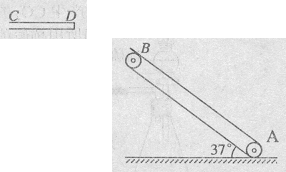
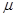 1=0.9,自A点沿传送带方向以某一初速度冲上传送带时,恰能水平落到水平台的D端,求物体甲的最大初速度vo1
1=0.9,自A点沿传送带方向以某一初速度冲上传送带时,恰能水平落到水平台的D端,求物体甲的最大初速度vo1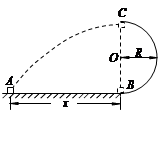
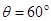 ,长为
,长为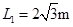 的倾斜轨道AB,通过微小圆弧与长为
的倾斜轨道AB,通过微小圆弧与长为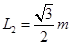 的水平轨道BC相连,然后在C处设计一个竖直完整的光滑圆轨道,出口为水平轨道D,如图所示。现将一个小球从距A点高为h="0.9" m的水平台面上以一定的初速度
的水平轨道BC相连,然后在C处设计一个竖直完整的光滑圆轨道,出口为水平轨道D,如图所示。现将一个小球从距A点高为h="0.9" m的水平台面上以一定的初速度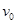 水平弹出,到A点时速度方向恰沿AB方向,并沿倾斜轨道滑下。已知小球与AB和BC间的动摩擦因数均为
水平弹出,到A点时速度方向恰沿AB方向,并沿倾斜轨道滑下。已知小球与AB和BC间的动摩擦因数均为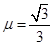 。
。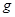 取10m/s2,求:
取10m/s2,求:
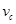 ;
;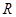 应该满足什么条件。
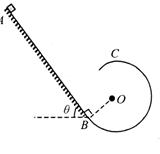
应该满足什么条件。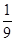 ×10-6C,如图所示,将小球B缓缓拉离竖直位置,当绳与竖直方向的夹角为60°时,将其由静止释放,小球B将在竖直面内做圆周运动.已知释放瞬间绳刚好张紧,但无张力.静电力常量
×10-6C,如图所示,将小球B缓缓拉离竖直位置,当绳与竖直方向的夹角为60°时,将其由静止释放,小球B将在竖直面内做圆周运动.已知释放瞬间绳刚好张紧,但无张力.静电力常量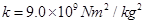 ,g取10m/s2。求
,g取10m/s2。求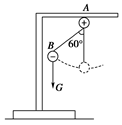
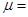
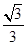 。(重力加速度g取10 m/s2)
。(重力加速度g取10 m/s2) 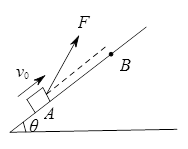
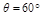 ,小球质量为m=0.5kg,D点与小孔A的水平距离s=2m,g取10m/s2。求:
,小球质量为m=0.5kg,D点与小孔A的水平距离s=2m,g取10m/s2。求: