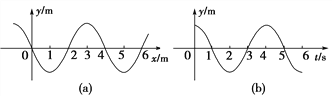
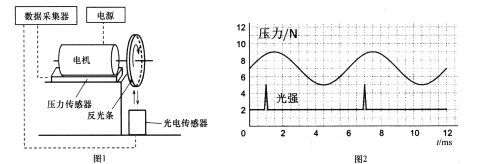
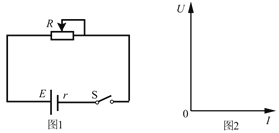
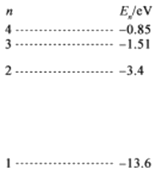题目内容
【题目】如图所示，M1 N1 P1Q1和M2 N2 P2 Q2为在同一水平面内足够长的金属导轨，处在磁感应强度B=2 T的匀强磁场中，磁场方向竖直向下。导轨的M1N1段与M2 N2段相互平行，间距为2 m; P1Q1段与P2 Q2段平行，间距为1m。两根质量均为m=lkg、电阻均为R=0.5Ω的金属杆a、b垂直于导轨放置，杆的长度恰好等于导轨间距。一根不可伸长的绝缘轻质细线一端系在金属杆6的中点，另一端绕过轻小定滑轮与质量为mc的重物c相连，线的水平部分与P1Q1平行且足够长，c离地面足够高。已知两杆与导轨间的动摩擦因数均为μ=0.4，不计导轨电阻及电磁辐射，重力加速度为g=10 m／s2。
(1)若要保持整个系统静止，重物f的质量不能超过多少？
(2)若c的质量改为mc=0. 6kg，将c由静止释放并开始计时，杆在运动过程中始终保持与轨道垂直且接触良好，求金属杆b的最大速度。
(3)在(2)的条件下，已知t=4 s时，金属杆b已经非常接近最大速度，求这4s的过程中a棒上产生的焦耳热。
【答案】(1)
；(2)v=0.5m/s(3)Q=1.7J
【解析】试题分析：根据平衡状态求出重物的质量最大值，由闭合电路欧姆定律和动量守恒定律、能量守恒定律列方程求解。
(1)b静止时，a一定也能静止，
对b、c受力平衡，有：
解得：；
(2)设b运动的最大速度
，回路的电流为I，此时细绳的拉力为
又
联立解得：
，I=1A
设a杆此时所受的安培力为
满足
感应电动势：
解得：
；
(3)分别对b和c，由动量定理
又
联立解得b的位移为
对a、b和c，能量守恒定律得
解得：
a上产生的焦耳热为
点晴：对于电磁感应问题研究思路常常有两条：一条从力的角度，重点是分析安培力作用下导体棒的平衡问题，根据平衡条件列出方程；另一条是能量，分析涉及电磁感应现象中的能量转化问题，根据动能定理、功能关系等列方程求解。
