题目内容
【题目】如图所示,质量为m1=0.5 kg、m2=0.2 kg的弹性小球A、B穿过一绕过定滑轮的轻绳,绳子末端与地面距离h=0.8 m,小球距离绳子末端l=6.5 m,不计绳子质量,忽略与定滑轮相关的摩擦力,g=10 m/s2。
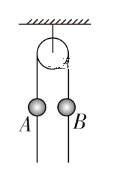
(1)若A,B两球固定在绳上,不会在绳上滑动 ,求释放瞬间绳中张力大小?
(2)若小球A、B与轻绳不固定,球与绳的滑动摩擦力都为重力的0.5倍。现在由静止同时释放A、B两个小球, 则释放A、B两个小球后,A、B的各自加速度多大?
(3)若同(2)问中条件,小球B从静止释放经多长时间落到地面?
【答案】(1)2.86N (2)a1=8 m/s2 a2=5 m/s2 (3)1.6 s
【解析】
(1)对A,B小球整体列牛顿运动定律方程:
![]() ,解得:
,解得:![]()
对B![]()
解得:![]()
(2)由题意知,B与轻绳的摩擦力小于A与轻绳的摩擦力。为保证A、B对轻绳的力相同,所以轻绳与A、B间的摩擦均为km2g。
对B,由牛顿第二定律得:m2g-km2g=m2a2,a2=5 m/s2
对A,由牛顿第二定律得:m1g-km2g=m1a1,a1=8 m/s2
(3)A球与绳子一起向下加速运动,B球沿绳子向下加速运动。
设经历时间t1小球B脱离绳子,小球B下落高度为h1,获得速度为v,
![]() ,解得:
,解得:![]()
![]()
v=a2t1=5 m/s
小球B脱离绳子后在重力作用下匀加速下落,此时距地面高为h2,经t2落地,则:
h2=6.5 m+0.8 m-2.5 m=4.8 m
![]() ,t2=0.6 s
,t2=0.6 s
![]()
解得:t2=-1.6s(舍去)t2=0.6s
t=t1+t2=1.6 s

练习册系列答案
相关题目