题目内容
如图所示,AB,CO为互相垂直的丁字形公路,CB为一斜直公路,CB与CO成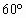 角,C,O间距离300m,一逃犯骑着摩托车以54km/h的速度正沿AB公路逃窜,当逃犯途经路口O处时,守候在C处的公安干警立即以1.2m/s2的加速度启动警车,警车所能达到的最大速度为108km/h.
角,C,O间距离300m,一逃犯骑着摩托车以54km/h的速度正沿AB公路逃窜,当逃犯途经路口O处时,守候在C处的公安干警立即以1.2m/s2的加速度启动警车,警车所能达到的最大速度为108km/h.
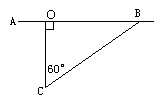
(1)若公安干警沿COB路径追捕逃犯,则经过多长时间在何处能将逃犯截获?
(2)若公安干警抄CB近路到达B处时,逃犯又以原速率掉头向相反方向逃窜,公安干警则继续沿BA方向追赶,则总共经多长时间在何处能将逃犯截获?(不考虑摩托车和警车转向的时间)
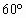 角,C,O间距离300m,一逃犯骑着摩托车以54km/h的速度正沿AB公路逃窜,当逃犯途经路口O处时,守候在C处的公安干警立即以1.2m/s2的加速度启动警车,警车所能达到的最大速度为108km/h.
角,C,O间距离300m,一逃犯骑着摩托车以54km/h的速度正沿AB公路逃窜,当逃犯途经路口O处时,守候在C处的公安干警立即以1.2m/s2的加速度启动警车,警车所能达到的最大速度为108km/h.
(1)若公安干警沿COB路径追捕逃犯,则经过多长时间在何处能将逃犯截获?
(2)若公安干警抄CB近路到达B处时,逃犯又以原速率掉头向相反方向逃窜,公安干警则继续沿BA方向追赶,则总共经多长时间在何处能将逃犯截获?(不考虑摩托车和警车转向的时间)
(1)45s;675m.(2)34.6s;456m.
:(1)摩托车的速度v=15m/s.警车的最大速度vm=30m/s,警车达到最大速度的时间t1= =25s,行驶的距离s1=
=25s,行驶的距离s1= t1=375m,
t1=375m,
在t1时间内摩托车行驶的距离 =vt1=375m,
=vt1=375m,
因为s1-CO=75m< ,故警车在t1时间内尚未追上摩托车,相隔距离Δs=
,故警车在t1时间内尚未追上摩托车,相隔距离Δs= -(s1-CO)=300m,
-(s1-CO)=300m,
设再经t2警车才能追上摩托车,则t2=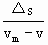 =20s,
=20s,
从而截获逃犯总共所需时间t=t1+t2=45s,
截获处在OB方向距O处距离为:s=vt=675m.
(2)由几何关系可知,CB=CO/cos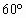 =600m,因s1<CB,故警车达到最大速度时尚未到达B点,设再经
=600m,因s1<CB,故警车达到最大速度时尚未到达B点,设再经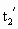 时间到达B点,则
时间到达B点,则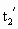 =
=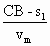 =7.5s,
=7.5s,
在(t1+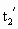 )时间内摩托车行驶的距离
)时间内摩托车行驶的距离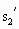 =v(t1+
=v(t1+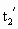 )=487.5m,此时摩托车距B处的距离为Δ
)=487.5m,此时摩托车距B处的距离为Δ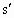 =OB-
=OB-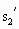 =OCtan
=OCtan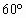 -
-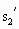 ≈32m,此后逃犯掉头向相反方向逃窜,设再经时间
≈32m,此后逃犯掉头向相反方向逃窜,设再经时间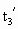 警车才能追上逃犯,则
警车才能追上逃犯,则
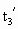 =
=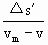 =2.1s,从而截获逃犯总共所需时间t=t1+
=2.1s,从而截获逃犯总共所需时间t=t1+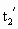 +
+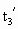 =34.6s.
=34.6s.
截获处在OB间与O点的距离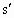 =v(t1+
=v(t1+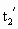 )-v
)-v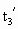 =456m.
=456m.
巧解分析:本题是将匀速直线运动和匀加速直线运动的知识应用到公安干警追捕逃犯的情景之中,让人感觉耳目一新,并体会到学以致用.
★ 试题错析: 思维诊断:本题要仔细分析警车和摩托车的运动过程,寻找两者在时间和路程上的联系.有关追赶问题还要注意有时两者具有相同速度时,是两者相距最远或最近或者两者刚好不相碰的临界条件
 =25s,行驶的距离s1=
=25s,行驶的距离s1= t1=375m,
t1=375m,在t1时间内摩托车行驶的距离
 =vt1=375m,
=vt1=375m,因为s1-CO=75m<
 ,故警车在t1时间内尚未追上摩托车,相隔距离Δs=
,故警车在t1时间内尚未追上摩托车,相隔距离Δs= -(s1-CO)=300m,
-(s1-CO)=300m,设再经t2警车才能追上摩托车,则t2=
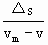 =20s,
=20s,从而截获逃犯总共所需时间t=t1+t2=45s,
截获处在OB方向距O处距离为:s=vt=675m.
(2)由几何关系可知,CB=CO/cos
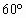 =600m,因s1<CB,故警车达到最大速度时尚未到达B点,设再经
=600m,因s1<CB,故警车达到最大速度时尚未到达B点,设再经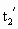 时间到达B点,则
时间到达B点,则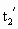 =
=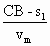 =7.5s,
=7.5s,在(t1+
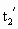 )时间内摩托车行驶的距离
)时间内摩托车行驶的距离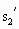 =v(t1+
=v(t1+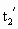 )=487.5m,此时摩托车距B处的距离为Δ
)=487.5m,此时摩托车距B处的距离为Δ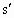 =OB-
=OB-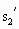 =OCtan
=OCtan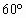 -
-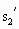 ≈32m,此后逃犯掉头向相反方向逃窜,设再经时间
≈32m,此后逃犯掉头向相反方向逃窜,设再经时间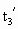 警车才能追上逃犯,则
警车才能追上逃犯,则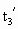 =
=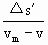 =2.1s,从而截获逃犯总共所需时间t=t1+
=2.1s,从而截获逃犯总共所需时间t=t1+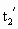 +
+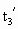 =34.6s.
=34.6s.截获处在OB间与O点的距离
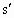 =v(t1+
=v(t1+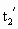 )-v
)-v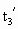 =456m.
=456m.巧解分析:本题是将匀速直线运动和匀加速直线运动的知识应用到公安干警追捕逃犯的情景之中,让人感觉耳目一新,并体会到学以致用.
★ 试题错析: 思维诊断:本题要仔细分析警车和摩托车的运动过程,寻找两者在时间和路程上的联系.有关追赶问题还要注意有时两者具有相同速度时,是两者相距最远或最近或者两者刚好不相碰的临界条件

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
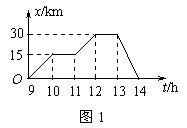
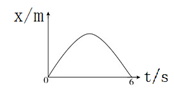
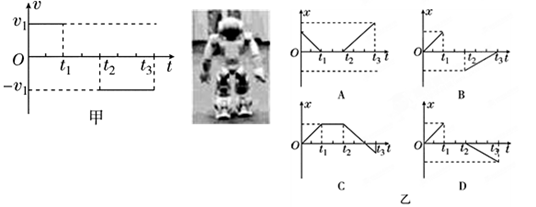
 的加速度匀加速开出.求:
的加速度匀加速开出.求: