题目内容
6. 我国研制的“嫦娥三号”月球探测器成功在月球表面实线软着陆,如图所示,探测器首先被送到距离月球表面高度为H的近月轨道做匀速圆周运动,之后在轨道上的A点实施变轨,使探测器绕月球做椭圆运动,当运动到B点时再次变轨,使探测器靠近月球表面,当其距离月球表面附近高度为h(h<5m)时开始做自由落体运动至月球表面,探测器携带的传感器测得自由落地运动时间为t,已知月球半径为R,万有引力常量为G,则下列说法正确的是( )
我国研制的“嫦娥三号”月球探测器成功在月球表面实线软着陆,如图所示,探测器首先被送到距离月球表面高度为H的近月轨道做匀速圆周运动,之后在轨道上的A点实施变轨,使探测器绕月球做椭圆运动,当运动到B点时再次变轨,使探测器靠近月球表面,当其距离月球表面附近高度为h(h<5m)时开始做自由落体运动至月球表面,探测器携带的传感器测得自由落地运动时间为t,已知月球半径为R,万有引力常量为G,则下列说法正确的是( )| A. | “嫦娥三号”在A点变轨时,需减速才能从近月圆轨道进入椭圆轨道 | |
| B. | 根据以上已知条件不能求出卫星在近月圆轨道的速度 | |
| C. | 根据以上已知条件可求出月球的质量为$\frac{{2h{R^2}}}{{G{t^2}}}$ | |
| D. | 探测器在近月圆轨道的周期比椭圆轨道上的周期小 |
分析 从近月圆轨道需要点火减速做近心运动才能进入椭圆轨道;由月球表面物体的引力等于“重力”,得到月球质量$M=\frac{{g{R^2}}}{G}$,根据自由落体运动下落高度为h,运动时间为t,由$h=\frac{1}{2}g{t^2}$得到$g=\frac{2h}{t^2}$代入上述月球的质量表达式中求出表达式即可判断正误.椭圆轨道的轨道半长轴和近月圆轨道的轨道半径不相等,因此周期不相同.
解答 解:A、“嫦娥三号”在椭圆轨道上的A点做向心运动,提供的万有引力大于需要的向心力,所以从近月圆轨道需要点火减速才能进入椭圆轨道,故A正确;
B、C、根据自由落体运动下落高度为h,运动时间为t,
由$h=\frac{1}{2}g{t^2}$得到$g=\frac{2h}{t^2}$;由月球表面物体的引力等于“重力”,得到月球质量$M=\frac{{g{R^2}}}{G}$=$\frac{{2h{R^2}}}{{G{t^2}}}$;
由题,探测器到月球球心的距离:r=H+R
根据万有引力提供向心力得:$\frac{MGm}{{r}^{2}}=\frac{m{v}^{2}}{r}$
所以:v=$\sqrt{\frac{GM}{r}}$=$\sqrt{\frac{g{R}^{2}}{R+H}}$.故B错误,C正确;
D、根据开普勒第三定律:$\frac{{R}^{3}}{{T}^{2}}=K$,可知探测器在近月圆轨道的周期比椭圆轨道上的周期大.故D错误.
故选:AC
点评 运用黄金代换式GM=gR2求出问题是考试中常见的方法;要记住球体的体积公式;明白第一宇宙速度的意义;可以将椭圆运动近似堪为圆周运动,其半径为轨道半长轴.

练习册系列答案
相关题目
17.机械运动在介质中传播形成机械波.下列说法正确的是( )
| A. | 如果波源停止振动,在介质中传播的波动也立即停止 | |
| B. | 在纵波中质点的振动方向总是垂直于波的传播方向 | |
| C. | 在横波中两个相邻的波峰(或波谷)之间的距离等于波长 | |
| D. | 横波中振动质点不随波迁移,纵波中振动质点随波迁移 |
14. 如图所示,把三个半径均为r,质量均为m的光滑小球置于截面为半圆形的槽内,三个小球均处于静止状态,已知槽的截面半径R=3r,重力加速度为g,则下列说法正确的是( )
如图所示,把三个半径均为r,质量均为m的光滑小球置于截面为半圆形的槽内,三个小球均处于静止状态,已知槽的截面半径R=3r,重力加速度为g,则下列说法正确的是( )
 如图所示,把三个半径均为r,质量均为m的光滑小球置于截面为半圆形的槽内,三个小球均处于静止状态,已知槽的截面半径R=3r,重力加速度为g,则下列说法正确的是( )
如图所示,把三个半径均为r,质量均为m的光滑小球置于截面为半圆形的槽内,三个小球均处于静止状态,已知槽的截面半径R=3r,重力加速度为g,则下列说法正确的是( )| A. | 三个小球与槽之间的作用力大小相等 | |
| B. | 球1与槽之间的作用力大小为mg | |
| C. | 球2与槽之间的作用力大小为3mg | |
| D. | 若仅增大槽的半径R,则球2与槽之间的作用力增大 |
1. 如图所示,质量为m的小车在水平恒力F推动下,从山坡底部A处由静止起运动至高为h的坡顶B,获得速度为v,AB的水平距离为s,在上述运动过程中,下列说法正确的是( )
如图所示,质量为m的小车在水平恒力F推动下,从山坡底部A处由静止起运动至高为h的坡顶B,获得速度为v,AB的水平距离为s,在上述运动过程中,下列说法正确的是( )
 如图所示,质量为m的小车在水平恒力F推动下,从山坡底部A处由静止起运动至高为h的坡顶B,获得速度为v,AB的水平距离为s,在上述运动过程中,下列说法正确的是( )
如图所示,质量为m的小车在水平恒力F推动下,从山坡底部A处由静止起运动至高为h的坡顶B,获得速度为v,AB的水平距离为s,在上述运动过程中,下列说法正确的是( )| A. | 小车克服阻力做功$\frac{1}{2}$mv2+mgh-Fs | B. | 小车的动能增加了Fs-mgh | ||
| C. | 小车的重力势能增加了mgh | D. | 小车的机械能增加了$\frac{1}{2}$mv2+mgh |
11.一颗子弹水平射入静止在光滑水平地面上的木块后不再穿出,木块的动能增加了20J,已知木块的质量小于子弹的质量,则此过程中产生的内能可能是( )
| A. | 18J | B. | 24J | C. | 32J | D. | 48J |
18. 某液体报警装置,电路图图所示.M为传感器,接触到液体时其电阻RM发生变化,导致S两端电压US增大,则装置发出警报.若发出警报则下列说法正确的是( )
某液体报警装置,电路图图所示.M为传感器,接触到液体时其电阻RM发生变化,导致S两端电压US增大,则装置发出警报.若发出警报则下列说法正确的是( )
 某液体报警装置,电路图图所示.M为传感器,接触到液体时其电阻RM发生变化,导致S两端电压US增大,则装置发出警报.若发出警报则下列说法正确的是( )
某液体报警装置,电路图图所示.M为传感器,接触到液体时其电阻RM发生变化,导致S两端电压US增大,则装置发出警报.若发出警报则下列说法正确的是( )| A. | 电压表读数减小,电流表读数增大 | B. | RM变大,且R越小,US增大越明显 | ||
| C. | RM变大,电压表读数变大 | D. | RM变小,且R越大,US增大越明显 |
14.跳高比赛中,必须在运动员着地处铺上很厚的海绵垫子,这是为了( )
| A. | 减小运动员着地过程中受到的冲量作用 | |
| B. | 减小运动员着地过程中受到的平均冲力 | |
| C. | 减小运动员着地过程中动量的变化量 | |
| D. | 减小运动员的惯性 |
13.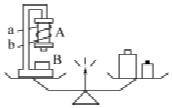 如图所示为一台非铁性物质制成的天平,天平左盘中的A是螺线管,B是铁块,螺线管未通电时天平平衡,现使螺线管a端接直流电源负极,b端接正极,调节螺线管中电流的大小,使铁块B向上加速运动,在B向上运动的过程中,下列判断正确的是( )
如图所示为一台非铁性物质制成的天平,天平左盘中的A是螺线管,B是铁块,螺线管未通电时天平平衡,现使螺线管a端接直流电源负极,b端接正极,调节螺线管中电流的大小,使铁块B向上加速运动,在B向上运动的过程中,下列判断正确的是( )
 如图所示为一台非铁性物质制成的天平,天平左盘中的A是螺线管,B是铁块,螺线管未通电时天平平衡,现使螺线管a端接直流电源负极,b端接正极,调节螺线管中电流的大小,使铁块B向上加速运动,在B向上运动的过程中,下列判断正确的是( )
如图所示为一台非铁性物质制成的天平,天平左盘中的A是螺线管,B是铁块,螺线管未通电时天平平衡,现使螺线管a端接直流电源负极,b端接正极,调节螺线管中电流的大小,使铁块B向上加速运动,在B向上运动的过程中,下列判断正确的是( )| A. | 螺线管A的上端为S极,天平仍保持平衡 | |
| B. | 螺线管A的上端为S极,天平右盘下降 | |
| C. | 螺线管A的下端为S极,天平左盘下降 | |
| D. | 螺线管A的下端为S极,无法判断天平是否平衡 |
 );若以相等时间间隔在该直尺的另一面标记出表示反应时间的刻度线,则每个时间间隔在直尺上对应的长度是_________的(填“相等”或“不相等”)
);若以相等时间间隔在该直尺的另一面标记出表示反应时间的刻度线,则每个时间间隔在直尺上对应的长度是_________的(填“相等”或“不相等”)