题目内容
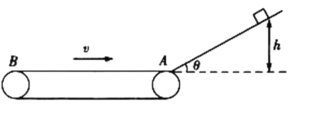
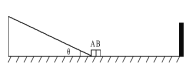
【题目】如图所示，竖直平面内一足够长、倾角θ=30的固定光滑倾斜轨道与一水平轨道通过一小段光滑圆弧平滑连接，静止在水平轨道最左端的两个可视为质点的小物块A、B，质量分别为mA=2kg、mB=1kg， 两者之间有一被压缩的微型弹簧，弹簧具有的弹性势能EP=3J，A与地面的动摩擦因数为μA=0.2，B与右侧竖直墙壁的距离L=0.5m。某时刻将压缩的弹簧释放，使A、B瞬间分离，B沿着水平轨道与墙壁垂直的方向向右运动。（若运动过程中涉及到碰撞，均为弹性碰撞且碰撞时间极短，重力加速度g =10m/s2 。）
（1）求释放后瞬间A、B速度的大小；
（2）若释放后A、B不再发生碰撞且恰好停在同一位置，求B与地面间动摩擦因数μB。
【答案】（1）
；
（2）
或
【解析】
(1)由动量守恒得：
由能量守恒得：
解得：
；
(2)不再发生碰撞，A在斜面上往返运动最后停在水平面上某点，设该点为O点，A的位移为xA，由动能定理可得：
(或 A在斜面上往返运动，再次运动到水平面的速度大小仍为 ，A在水平面上运动的加速度：
位移
则B在水平面上运动的位移
若B不与墙壁碰撞：
（或
； 
）
得
若B与墙壁碰撞1次后返回：B在水平面上运动的路程：
由
得
A在斜面上往返运动，由牛顿第二定律得：
得
A在斜面上运动的时间：
由于B被弹开后与墙壁碰撞再运动到斜面底端的最短时间
＞
，
故B不能运动到斜面上再返回停在O点 ，也不能与墙壁发生第二次碰撞，故B与地面动摩擦因数或
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
