Question

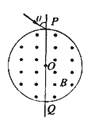
【题目】如图所示，一定滑轮上绕有轻质柔软细线，线的一端系一质量为3m的重物，另一端系一质量为m、电阻为r的金属杆。在竖直平面内有间距为L的足够长的平行金属导轨PQ、EF，在QF之间连接有阻值为R的电阻，其余电阻不计，磁感应强度为B0的匀强磁场与导轨平面垂直。开始时金属杆置于导轨下端QF处，将重物由静止释放，当重物下降h时恰好达到稳定速度而匀速下降。运动过程中金属杆始终与导轨垂直且接触良好，(忽略摩擦阻力，重力加速度为g)，则

A．电阻R中的感应电流方向QF

B．重物匀速下降的速度

C．重物从释放到下降h的过程中，重物机械能的减少量大于回路中产生的焦耳热

D．若将重物下降h时的时刻记作t=0，速度记为v0，从此时刻起，磁感应强度逐渐减小，使金属杆中恰好不再产生感应电流，则磁感应强度B随时间t变化的关系式

Answer 1

【答案】ACD

【解析】

试题分析：导体棒向上运动过程中，根据楞次定律，可知，通过电阻R的感应电流方向QF，A正确；导体棒匀速下降时，根据受力平衡：，因此重物匀速下降的速度，B错误；重物从释放到下降h的过程中，重物机械能的减少量一部分转化为导体棒的机械能，另一部分转化为焦耳热，C正确；若刚好达到最大速度时开始计时，此时速度计为，若回路中不再产生电磁感应现象，则磁通量为恒量，即：，而此过程中设绳子拉力为T，则对物体，对导体棒，可求出加速度，代入上式可得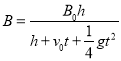：，D正确。