题目内容
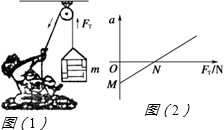
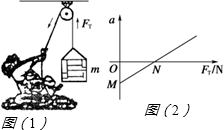 如图(1)所示,某人借助定滑轮将质量为m的货物提升到高处,测得货物加速度a与绳子对货物拉力FT之间的函数关系如图(2)所示.不计滑轮的摩擦,则:
如图(1)所示,某人借助定滑轮将质量为m的货物提升到高处,测得货物加速度a与绳子对货物拉力FT之间的函数关系如图(2)所示.不计滑轮的摩擦,则:(1)图线与横轴的交点N数值的含义为:
mg
mg
;(2)图线斜率的含义为:
物体质量的倒数
| 1 |
| m |
物体质量的倒数
.| 1 |
| m |
分析:货物受到重力和拉力作用,根据牛顿第二定律得到a与FT关系表达式,运用数学知识分析截距和斜率的意义.
解答:解:货物受到重力和拉力作用,根据牛顿第二定律得
FT-mg=ma
变形得到 a=
-g
当a=0时,FT=mg,即线与横轴的交点N数值的含义为mg;
由数学知识可知 a-FT图象是直线,其斜率等于
.
故答案为:mg;
.
FT-mg=ma
变形得到 a=
| FT |
| m |
当a=0时,FT=mg,即线与横轴的交点N数值的含义为mg;
由数学知识可知 a-FT图象是直线,其斜率等于
| 1 |
| m |
故答案为:mg;
| 1 |
| m |
点评:本题考查理解物理图象的能力.对于图象,往往要从物理规律进行推导,得出解析式,再应用数学知识理解其物理意义.

练习册系列答案
相关题目
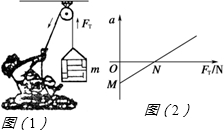 如图(1)所示,某人借助定滑轮将质量为m的货物提升到高处,测得货物加速度a与绳子对货物拉力FT之间的函数关系如图(2)所示.不计滑轮的摩擦,则:
如图(1)所示,某人借助定滑轮将质量为m的货物提升到高处,测得货物加速度a与绳子对货物拉力FT之间的函数关系如图(2)所示.不计滑轮的摩擦,则: