题目内容
8.小谢所在的实验小组测量小车从斜面上下滑所受到的阻力大小,他利用一打点计时器固定在斜面上某处,一小车拖着穿过打点计时器的纸带从斜面上滑下,如图甲所示.图乙是打出的纸带的一段,已量出各相邻计数点的长度分别为:S1、S2、S3、S4、S5、S6、S7、S8.
①已知打点计时器使用的交流电频率为f,则打下B点时小车的速度VB=$(\frac{{{s_1}+{s_2}}}{4})f$,小车下滑的加速度算式为a=$\frac{{{f^2}[({{s_5}+{s_6}+{s_7}+{s_8}})-({s_1}+{s_2}+{s_3}+{s_4})]}}{16}$(用题中所给的符号表示).
②已知当地的重力加速度为g,本实验中只有毫米刻度尺,没有量角器,为了求出小车在下滑过程中所受的阻力,还需测量的物理量有小车质量m,斜面上任意两点间距离l及这两点的高度差h (要用文字及符号表示).
③用加速度a及其他需要测得的量表示阻力的计算式为F阻=$mg\frac{h}{l}-ma$.
分析 ①匀变速直线运动中,平均速度等于中间时刻的瞬时速度,根据△x=aT2列式求解加速度;
②③根据牛顿第二定律列式求解阻力,确定待测量.
解答 解:①匀变速直线运动中,平均速度等于中间时刻的瞬时速度,故:
VB=$\frac{{x}_{AC}}{4T}$=($\frac{{s}_{1}+{s}_{2}}{4}$)f
根据公式△x=aT2,有:
(S5+S6+S7+S8)-(S1+S2+S3+S4)=a(4T)2
其中:T=$\frac{2}{f}$
解得:
a=$\frac{{{f^2}[({{s_5}+{s_6}+{s_7}+{s_8}})-({s_1}+{s_2}+{s_3}+{s_4})]}}{16}$,
②③根据牛顿第二定律,有:
mgsinθ-F阻=ma
解得:
F阻=mgsinθ-ma=mg$\frac{h}{l}$-ma
故还需要测量小车质量m、斜面上任意两点间距离l及这两点的高度差h;
故答案为:①$(\frac{{{s_1}+{s_2}}}{4})f$; $\frac{{{f^2}[({{s_5}+{s_6}+{s_7}+{s_8}})-({s_1}+{s_2}+{s_3}+{s_4})]}}{16}$,
②小车质量m; 斜面上任意两点间距离l及这两点的高度差h;
③$mg\frac{h}{l}-ma$.
点评 本题关键是明确小车的受力情况和运动性质,然后结合运动学公式和牛顿第二定律定律列式求解.

练习册系列答案
相关题目
19.一只小船在静水中的速度大小始终为5m/s,在流速为3m/s的河中航行(船头可沿任意方向),则河岸上的人能看到船的实际航速大小可能是( )
| A. | 3m/s | B. | 1m/s | C. | 12m/s | D. | 10m/s |
16. 如图所示,在光滑水平桌面的两端各固定一个定滑轮,用轻绳经过滑轮将弹簧分别与质量为m1=8kg、m2=2kg的两个物体A、B相连.不计绳与滑轮之间的摩擦及弹簧秤、定滑轮的质量,g取10m/s2,弹簧秤的读数为( )
如图所示,在光滑水平桌面的两端各固定一个定滑轮,用轻绳经过滑轮将弹簧分别与质量为m1=8kg、m2=2kg的两个物体A、B相连.不计绳与滑轮之间的摩擦及弹簧秤、定滑轮的质量,g取10m/s2,弹簧秤的读数为( )
 如图所示,在光滑水平桌面的两端各固定一个定滑轮,用轻绳经过滑轮将弹簧分别与质量为m1=8kg、m2=2kg的两个物体A、B相连.不计绳与滑轮之间的摩擦及弹簧秤、定滑轮的质量,g取10m/s2,弹簧秤的读数为( )
如图所示,在光滑水平桌面的两端各固定一个定滑轮,用轻绳经过滑轮将弹簧分别与质量为m1=8kg、m2=2kg的两个物体A、B相连.不计绳与滑轮之间的摩擦及弹簧秤、定滑轮的质量,g取10m/s2,弹簧秤的读数为( )| A. | 32N | B. | 48N | C. | 60N | D. | 80N |
13. 如图所示,一质量为m的物体在沿斜面向上的恒力F作用下,由静止从底端向上做匀加速直线运动.若斜面足够长,表面光滑,倾角为θ.经时间t恒力F做功80J,此后撤去恒力F,物体又经时间t回到出发点,且回到出发点时的速度大小为v,若以地面为重力势能的零势能面,则下列说法中正确的是( )
如图所示,一质量为m的物体在沿斜面向上的恒力F作用下,由静止从底端向上做匀加速直线运动.若斜面足够长,表面光滑,倾角为θ.经时间t恒力F做功80J,此后撤去恒力F,物体又经时间t回到出发点,且回到出发点时的速度大小为v,若以地面为重力势能的零势能面,则下列说法中正确的是( )
 如图所示,一质量为m的物体在沿斜面向上的恒力F作用下,由静止从底端向上做匀加速直线运动.若斜面足够长,表面光滑,倾角为θ.经时间t恒力F做功80J,此后撤去恒力F,物体又经时间t回到出发点,且回到出发点时的速度大小为v,若以地面为重力势能的零势能面,则下列说法中正确的是( )
如图所示,一质量为m的物体在沿斜面向上的恒力F作用下,由静止从底端向上做匀加速直线运动.若斜面足够长,表面光滑,倾角为θ.经时间t恒力F做功80J,此后撤去恒力F,物体又经时间t回到出发点,且回到出发点时的速度大小为v,若以地面为重力势能的零势能面,则下列说法中正确的是( )| A. | 物体回到出发点时的机械能是80 J | |
| B. | 在撤去力F前的瞬间,力F的功率是$\frac{2}{3}$mgvsinθ | |
| C. | 撤去力F前的运动过程中,物体的重力势能一直在增加,撤去力F后的运动过程中物体的重力势能一直在减少 | |
| D. | 撤去力F前的运动过程中,物体的动能一直在增加,撤去力F后的运动过程中物体的动能一直在减少 |
20.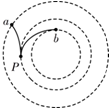 图中虚线是某电场中的一簇等势线.两个带电粒子从P点均沿等势线的切线方向射入电场,粒子运动的部分轨迹如图中实线所示.若粒子仅受电场力的作用,下列说法中正确的是( )
图中虚线是某电场中的一簇等势线.两个带电粒子从P点均沿等势线的切线方向射入电场,粒子运动的部分轨迹如图中实线所示.若粒子仅受电场力的作用,下列说法中正确的是( )
 图中虚线是某电场中的一簇等势线.两个带电粒子从P点均沿等势线的切线方向射入电场,粒子运动的部分轨迹如图中实线所示.若粒子仅受电场力的作用,下列说法中正确的是( )
图中虚线是某电场中的一簇等势线.两个带电粒子从P点均沿等势线的切线方向射入电场,粒子运动的部分轨迹如图中实线所示.若粒子仅受电场力的作用,下列说法中正确的是( )| A. | 两粒子的电性一定相反 | |
| B. | a点的电势高于b点的电势 | |
| C. | 粒子从P运动到a的过程中,电势能增大 | |
| D. | 粒子从P运动到b的过程中,动能增大 |
17. 如图是两等量异号点电荷,以两电荷连线的中点O为圆心画一半圆,在半圆上有a、b、c三点,b点在两电荷连线的垂直平分线上,下列说法正确的是( )
如图是两等量异号点电荷,以两电荷连线的中点O为圆心画一半圆,在半圆上有a、b、c三点,b点在两电荷连线的垂直平分线上,下列说法正确的是( )
 如图是两等量异号点电荷,以两电荷连线的中点O为圆心画一半圆,在半圆上有a、b、c三点,b点在两电荷连线的垂直平分线上,下列说法正确的是( )
如图是两等量异号点电荷,以两电荷连线的中点O为圆心画一半圆,在半圆上有a、b、c三点,b点在两电荷连线的垂直平分线上,下列说法正确的是( )| A. | a、c两点的电场强度相同 | |
| B. | a、c两点的电势相同 | |
| C. | 正电荷在a点的电势能大于在b点的电势能 | |
| D. | 将正电荷由O移到b电场力做正功 |
 如图所示,让小球从图中的C位置由静止开始摆下,摆到最低点D处,摆线刚好从与小球拴接处被拉断,并立即撤去摆线,小球在粗糙的水平面上由D点向D做匀减速运动,到达小孔A进入半径R=0.3m的竖直放置的光滑竖直圆弧轨道,当小球进入圆轨道立即关闭A孔,已知摆线长L=2m,θ=60°,小球质量为m=0.5kg,小球与粗糙水平面动摩擦因数μ=$\frac{1}{8}$,g取10m/s2.求:
如图所示,让小球从图中的C位置由静止开始摆下,摆到最低点D处,摆线刚好从与小球拴接处被拉断,并立即撤去摆线,小球在粗糙的水平面上由D点向D做匀减速运动,到达小孔A进入半径R=0.3m的竖直放置的光滑竖直圆弧轨道,当小球进入圆轨道立即关闭A孔,已知摆线长L=2m,θ=60°,小球质量为m=0.5kg,小球与粗糙水平面动摩擦因数μ=$\frac{1}{8}$,g取10m/s2.求: 某质点以初速度v0=2 m/s从坐标原点O沿x正方向做匀加速直线运动,其运动的加速度a=2m/s2,求:
某质点以初速度v0=2 m/s从坐标原点O沿x正方向做匀加速直线运动,其运动的加速度a=2m/s2,求: