Question

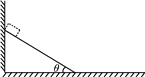
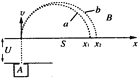
【题目】如图a所示，一根水平长杆固定不动，一个质量m=1.2kg的小环静止套在杆上，环的直径略大于杆的截面直径，现用斜面向上53°的拉力F作用于小环，将F从零开始逐渐增大，小环静止一段时间后开始被拉动，得到小环的加速度a与拉力F的图象如图b所示，加速度在F达到15N后保持不变．（g=10m/s2，sin53°=0.8，cos53°=0.6）求：

(1)F=15N时长杆对小球的弹力大小，及小环加速度的大小．

(2)F从0N增大到15N的过程中，F的最大功率240W，求小环在此过程的最大速度．

(3)环和长杆的动摩擦因数．

Answer 1

【答案】(1) 0, 7.5m/s2 (2) (3) μ=0.75

【解析】

(1)将F分解到竖直和水平两个方向，求得竖直分分力，由重力比较，求杆对小球的弹力．由牛顿第二定律求环的加速度．

(2)小环的加速度始终为正，小环的速度不断增大，则当F=15N时速度最大，功率最大，由P=Fvcosθ求小环在此过程的最大速度．

(3)F超过15N后，加速度不变，根据牛顿第二定律得到加速度的表达式，再进行解答．

(1)F=15N时，分解F可知，F竖直向上的分力大小为 Fsin53°=15×0.8N=12N=mg

所以杆与环间无弹力，杆对小球的弹力大小为0．

根据牛顿第二定律得 Fcos53°=ma

解得 a=7.5m/s2

(2)环的加速度始终为正，小环的速度不断增大，则当F=15N时速度最大，功率最大，

由P=Fvcos53°得：

最大速度为

(3)当F超过15N以后，由牛顿第二定律得Fcos53°-μ（Fsin53°-mg）=ma

因为a与F无关，所以有 Fcos53°=μ（Fsin53°

解得: μ=0.75