题目内容
4.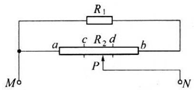 如图所示.电阻R1=6Ω,R2为滑动变阻器末接入电路时两固定端a、b之间的电阻,c、d两点将R2等分为三段.按图接好电路后,发现将滑片P分别滑到c点和d点时,M、N间电路的等效电阻之比为3:4.把上述电路的M、N两端接到电动势为E、内电阻为r的电源两极上.当滑片P位于d点时,R2上损耗的电功率P1=36W.如果P移到b端.那么R1上损耗的电功率P2≥36W.求电动势E和内电阻r的取值条件.
如图所示.电阻R1=6Ω,R2为滑动变阻器末接入电路时两固定端a、b之间的电阻,c、d两点将R2等分为三段.按图接好电路后,发现将滑片P分别滑到c点和d点时,M、N间电路的等效电阻之比为3:4.把上述电路的M、N两端接到电动势为E、内电阻为r的电源两极上.当滑片P位于d点时,R2上损耗的电功率P1=36W.如果P移到b端.那么R1上损耗的电功率P2≥36W.求电动势E和内电阻r的取值条件.
分析 结合将滑片P分别滑到c点和d点时,M、N间电路的等效电阻之比为3:4,根据串、并联电阻的特点列式,求R2.根据当滑片P位于d点时,R2上损耗的电功率P1=36W,由功率公式求通过R2的电流和总电流I.再根据P移到b端,R1上损耗的电功率P2≥36W,列式求解.
解答 解:据题意得:$\frac{({R}_{1}+\frac{2}{3}{R}_{2})•\frac{1}{3}{R}_{2}}{{R}_{1}+{R}_{2}}$:$\frac{({R}_{1}+\frac{1}{3}{R}_{2})•\frac{2}{3}{R}_{2}}{{R}_{1}+{R}_{2}}$=3:4
解得 R2=3R1=18Ω
当滑片P位于d点时,设R1中电流为I1,R2的ad段中的电流为I2,此时有 I1=I2,则有:
I12•$\frac{1}{3}{R}_{2}$+I22•$\frac{2}{3}{R}_{2}$=I22•R2=36W
解得 I2=$\sqrt{2}$A
干路电流 I=I1+I2=2$\sqrt{2}$A
因此 E=I($\frac{1}{2}×\frac{2}{3}{R}_{2}$+r)=2$\sqrt{2}$(6+r)①
P移到b端时,设MN间的电压为U,则 P2=$\frac{{U}^{2}}{{R}_{1}}$≥36W
可得 U≥6$\sqrt{6}$V
而 RMN=$\frac{{R}_{1}{R}_{2}}{{R}_{1}+{R}_{2}}$=4.5Ω
因此 E=U+$\frac{U}{{R}_{MN}}$r≥6$\sqrt{6}$+$\frac{6\sqrt{6}}{4.5}$r ②
由①②两式解得 r≤3$\sqrt{3}$Ω,且r>0
所以E、r取值满足的条件是:$\left\{\begin{array}{l}{E=2\sqrt{2}(6+r)}\\{0<r≤3\sqrt{3}Ω}\end{array}\right.$
答:E、r取值满足的条件是:$\left\{\begin{array}{l}{E=2\sqrt{2}(6+r)}\\{0<r≤3\sqrt{3}Ω}\end{array}\right.$.
点评 本题首先要搞清电路的连接关系,掌握串、并联电路总电阻的求法,以及总功率与各个电阻功率的关系.

 天天向上口算本系列答案
天天向上口算本系列答案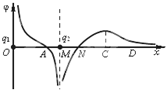 两电荷量分别为q1和q2的点电荷放在x轴上的 O、M两点,两电荷连线上各点电势φ随x变化的关系如图所示,其中A、N两点的电势均为零,ND段中的C点电势最高,则( )
两电荷量分别为q1和q2的点电荷放在x轴上的 O、M两点,两电荷连线上各点电势φ随x变化的关系如图所示,其中A、N两点的电势均为零,ND段中的C点电势最高,则( )| A. | N点的电场强度大小为零 | |
| B. | q1 小于q2 | |
| C. | NC间场强方向向x轴正方向 | |
| D. | 将负点电荷从N点移到D点,电场力先做正功后做负功 |
 如图所示电路图中,电源内阻不能忽略,R1=10Ω,R2=8Ω.当开关S板到位置1时,电压表的读数为2.0V,当开关S板到位置2时,电压表的读数可能是( )
如图所示电路图中,电源内阻不能忽略,R1=10Ω,R2=8Ω.当开关S板到位置1时,电压表的读数为2.0V,当开关S板到位置2时,电压表的读数可能是( )| A. | 2.2V | B. | 1.9V | C. | 1.6V | D. | 1.4V |
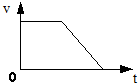
| A. | 物体最后回到了起点 | |
| B. | 物体开始静止,然后向山下滚,最后静止 | |
| C. | 物体先以恒定的速度运动,然后逐渐变慢,最后静止 | |
| D. | 物体的速度方向不变 |
| A. | 电动势E的大小等于单位时间内非静电力所做的功 | |
| B. | 电动势E是由电源本身决定的,跟电源的体积和外电路均无关 | |
| C. | 电动势E的单位与电势、电势差的单位都是伏特,故三者本质上一样 | |
| D. | 电动势E是表征电源把其他形式的能转化为电能本领的物理量 |
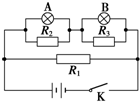 如图所示的电路中吗,灯泡A和B原来都是正常发光.忽然灯泡B比原来变暗了些,而灯泡A比原来变亮了些,试判断电路中什么地方出现的何种故障?(设只有一处出现了故障)R2断路.
如图所示的电路中吗,灯泡A和B原来都是正常发光.忽然灯泡B比原来变暗了些,而灯泡A比原来变亮了些,试判断电路中什么地方出现的何种故障?(设只有一处出现了故障)R2断路.
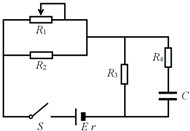 如图所示,电源电动势E=12V,内阻r=5Ω,滑动变阻器的最大阻值R1=20Ω,定值电阻R2=R3=3Ω,R4=2Ω,电容器的电容C=30μF.开关S闭合电路稳定后,求:
如图所示,电源电动势E=12V,内阻r=5Ω,滑动变阻器的最大阻值R1=20Ω,定值电阻R2=R3=3Ω,R4=2Ω,电容器的电容C=30μF.开关S闭合电路稳定后,求: