题目内容
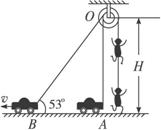
 摄制组在某大楼边拍摄武打片,要求特技演员从地面飞到屋顶.如图所示,若特技演员的质量m=50kg,导演在该房顶离地H=12m处架设了滑轮(大轮与小轮有相同的角速度),大轮和小轮的直径之比为3:2(人和车均视为质点,且轮直径远小于H),若轨道车从图中A匀速前进到B,在B处时,速度v=10m/s,绳BO与水平方向的夹角为53°,则由于绕在小轮上细钢丝的拉动,使演员由地面从静止开始向上运动.在车从A运动到B的过程中(g取10m/s2,sin53°=0.8,cos53°=0.6)( )
摄制组在某大楼边拍摄武打片,要求特技演员从地面飞到屋顶.如图所示,若特技演员的质量m=50kg,导演在该房顶离地H=12m处架设了滑轮(大轮与小轮有相同的角速度),大轮和小轮的直径之比为3:2(人和车均视为质点,且轮直径远小于H),若轨道车从图中A匀速前进到B,在B处时,速度v=10m/s,绳BO与水平方向的夹角为53°,则由于绕在小轮上细钢丝的拉动,使演员由地面从静止开始向上运动.在车从A运动到B的过程中(g取10m/s2,sin53°=0.8,cos53°=0.6)( )分析:本题A的关键是明确连在大滑轮的演员上升的高度与连在小滑轮的绳子变化长度的关系;B的关键是明确(连在小滑轮)车速在沿绳子方向的速度与(连在大滑轮)演员上升速度的关系;C的关键是利用机械能的公式即可求解;D的关键是根据动能定理即可求解.
解答:解:A、根据题意演员上升的高度为△h=(OB-OA)?
=(
-H)?
=4.5m,所以A错误.
B、将车速v沿着绳子方向和垂直于绳子的方向分解可知,在沿着绳子方向的速度为
=v?cosθ,所以人上升的速度
=
?
=
vcosθ,显然当θ=53°时人的速度最大为
=
×10×0.6m/s=9m/s,所以B错误.
C、人的最大机械能为E=mg△h+
,代入数据可得E=4275J,所以C错误.
D、对演员由动能定理有:
-mg△h=
-0,解得W=4275J,所以D正确.
故选D.
| 3 |
| 2 |
| H |
| sin53° |
| 3 |
| 2 |
B、将车速v沿着绳子方向和垂直于绳子的方向分解可知,在沿着绳子方向的速度为
| v | ∥ |
| v | 人 |
| v | ∥ |
| 3 |
| 2 |
| 3 |
| 2 |
| v | m |
| 3 |
| 2 |
C、人的最大机械能为E=mg△h+
| 1 |
| 2 |
| mv | 2 m |
D、对演员由动能定理有:
| W |
| 1 |
| 2 |
| mv | 2 m |
故选D.
点评:注意在涉及同轮缘滑轮问题中要抓住“应将物体的实际速度沿绳子方向和垂直绳子方向分解,物体在沿绳子方向的速度相等”,遇到像本题不同轮缘问题注意两轮直径关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 摄制组在某大楼边拍摄武打片,要求特技演员从地面飞到屋顶,如图所示,若特技演员的质量m=50kg(人和车可视为质点),g取10m/s2,导演在某房顶离地H=8m处架设了轮轴,轮和轴的直径之比为2:1.若轨道车从图中A前进s=6m到B处时速度为v=5m/s,则由于绕在轮上细钢丝拉动,特技演员( )
摄制组在某大楼边拍摄武打片,要求特技演员从地面飞到屋顶,如图所示,若特技演员的质量m=50kg(人和车可视为质点),g取10m/s2,导演在某房顶离地H=8m处架设了轮轴,轮和轴的直径之比为2:1.若轨道车从图中A前进s=6m到B处时速度为v=5m/s,则由于绕在轮上细钢丝拉动,特技演员( )