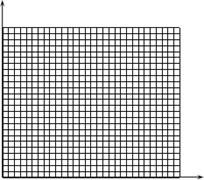题目内容
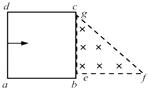
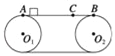
【题目】如图所示,在光滑的水平桌面上有一长为L=2m的木板C,它的两端各有一块挡板,C的质量为mC=5kg,在C的中央并排放着两个可视为质点的滑块A与B,其质量分别为mA=1kg、mB=4kg,开始时A、B、C均处于静止状态,并且A、B间夹有少许炸药,炸药爆炸使得A以vA=6m/s的速度水平向左运动,不计一切摩擦,两滑块中任一块与挡板碰撞后就与挡板合成一体,爆炸与碰撞时间不计,求:![]()
(1)当两滑块都与挡板碰撞后,板C的速度多大?
(2)从爆炸开始到两个滑块都与挡板碰撞为止,板C的位移多大?方向如何?
【答案】
(1)解:炸药爆炸,滑块A与B分别获得向左和向右的速度,由动量守恒可知,A的速度较大(A的质量小),A、B均做匀速运动,A先与挡板相碰合成一体(满足动量守恒)一起向左匀速运动,最终B也与挡板相碰合成一体(满足动量守恒),整个过程满足动量守恒.
整个过程A、B、C系统动量守恒,有:
0=(mA+mB+mC)v,
所以v=0
答:板C的速度是
(2)解:炸药爆炸,A、B获得的速度大小分别为vA、vB.以向左为正方向,有:
mAvA﹣mBvB=0,
解得:vB=1.5m/s,方向向右
然后A向左运动,与挡板相撞并合成一体,共同速度大小为vAC,
由动量守恒,有:
mAvA=(mA+mC)vAC,
解得:vAC=1m/s
此过程持续的时间为:t1= ![]() =
= ![]() s
s
此后,设经过t2时间B与挡板相撞并合成一体,则有:
![]() =vACt2+vB(t1+t2),解得:t2=0.3s
=vACt2+vB(t1+t2),解得:t2=0.3s
所以,板C的总位移为:xC=vACt2=0.3m,方向向左
答:板C的位移大小是0.3m,方向向左.
【解析】1、炸药爆炸,整个过程满足动量守恒,列出等式求解.2、炸药爆炸,A、B获得的速度大小关系可以根据动量守恒求得,A向左运动,与挡板相撞并合成一体由动量守恒求得共同速度,根据运动学公式求解.
【考点精析】利用动量守恒定律对题目进行判断即可得到答案,需要熟知动量守恒定律成立的条件:系统不受外力或系统所受外力的合力为零;系统所受的外力的合力虽不为零,但系统外力比内力小得多;系统所受外力的合力虽不为零,但在某个方向上的分量为零,则在该方向上系统的总动量的分量保持不变.

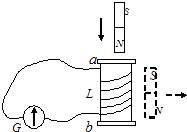
【题目】在探究加速度与物体所受合外力和质量间的关系时,采用如图所示的实验装置,小车及车中的砝码质量用M表示,盘及盘中的砝码质量用m表示,小车的加速度可由小车后拖动的纸带由打点计数器打上的点计算出:
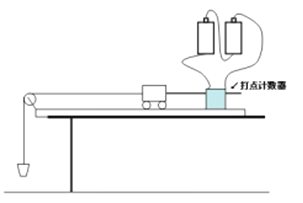
(1)某学生将实验装置如上图安装好,准备接通电源后开始做实验,但他的装置图中有两个明显的错误:
① ;
② 。
(2)M与m的大小关系满足 时,可以认为绳子对小车拉力的大小等于盘和砝码的重力。
(3)一组同学保持盘及盘中的砝码质量一定,探究物体加速度与质量的关系,以下做法错误的是( )
A.平衡摩擦力时,应将盘及盘中的砝码用细绳通过定滑轮系在小车上 |
B.每次改变小车的质量时,不需要重新平衡摩擦力 |
C.实验时,先放开小车,再接通打点计时器电源 |
D.小车运动的加速度,可用天平称出盘及砝码质量m、小车质量M,用a=mg/M求出 |
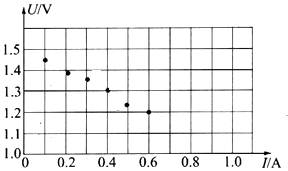
(4)在“探究加速度与质量的关系”时,保持砝码质量不变,改变小车质量m,得到的实验数据如下表:为了验证猜想,请在坐标系中作出最能直观反映a与m之间关系的图象.
实验次数 | 1 | 2 | 3 | 4 | 5 |
小车加速度a/ms-2 | 0.77 | 0.38 | 0.25 | 0.19 | 0.16 |
小车质量m/kg | 0.20 | 0.40 | 0.60 | 0.80 | 1.00 |