题目内容
18.图甲为阿特伍德机的示意图(不含光电门),它是早期测量重力加速度的器械,由英国数学家、物理学家阿特伍德于1784年制成,他将质量均为M的重物用细绳连接后,放在光滑的轻质滑轮上,处于静止状态,再在一个重物上附加一质量为m的小重物,这时由于小重物的重力而使系统做初速度为零的缓慢加速运动,测出其微小的加速度a,就可计算出重力加速度.(计算结果保留2位有效数字)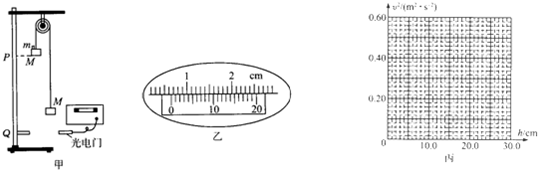
(1)依据实验原理,重力加速度可表示为g=$\frac{2M+m}{m}a$.
(用物理量m、M、a表示)
(2)为测量物体下落的加速度,某同学在阿特伍德机的竖直杆上的Q点加装了光电门,用其测量左侧物体经过光电门时的挡光时间△t,让物体从与杆上的另一点P同一高度处由静止下落,用h表示P、Q两点的高度差,用L表示左侧物体遮光部分的长度.
①用游标为20分度的卡尺测量L时如图乙所示,则L=0.640cm;
②某次实验中用光电门测出△t=1.85×10-2 s,则物体通过光电门时的速率v=0.35m/s;
③多次改变光电门的位置Q,每次均令物体从P点由静止开始运动,测量相应的h和△t的值,并计算出物体经过光电门时的瞬时速度.下表是记录的几组实验数据,请根据实验数据在图丙中作出v2-h的图象;
| v2/(m2•a-2) | 0.160 | 0.241 | 0.320 | 0.401 | 0.479 |
| h/m | 10.0 | 15.0 | 20.0 | 25.0 | 30.0 |
分析 (1)对整体应用牛顿第二定律求解加速度;
(2)①游标卡尺的读数等于主尺读数加上游标读数,不需估读,②根据极短时间内的平均速度等于瞬时速度求出小球通过光电门的速度,③根据描点法作出图象,④根据2ah=v2可知,v2-h的图象的斜率k=2a,根据图象求出斜率即可求解a.
解答 解:(1)对整体分析,整体所受的合力大小为mg,则整体的加速度a=$\frac{mg}{2M+m}$,解得g=$\frac{2M+m}{m}a$,
(2)①游标卡尺的固定刻度读数为6mm,游标读数为0.05×8mm=0.40mm,
所以最终读数为:L=6mm+0.40mm=6.40mm=0.640cm,
②极短时间内的平均速度表示瞬时速度,则
滑块经过光电门时的速度表达式v=$\frac{L}{△t}=\frac{0.64×1{0}^{-2}}{1.85×1{0}^{-2}}$m/s≈0.35m/s.
③根据描点法做作出v2-h的图象,如图所示:
④物体下落过程中,根据2ah=v2可知,v2-h的图象的斜率k=2a,
则2a=$\frac{0.40-0}{0.25-0}$=1.6m/s2.
解得:a=0.80m/s2.
故答案为:(1)$\frac{2M+m}{m}a$,(2)①0.640,0.35,③如图所示,④0.80.
点评 解答本题知道游标卡尺的读数方法,注意不需要估读,知道极短时间的平均速度可以表示瞬时速度,能够根据描点法作图,注意偏离图象很远的点直接舍去,知道图线斜率的物理意义,难度适中.

练习册系列答案
相关题目
8.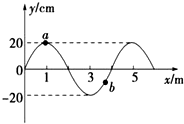 如图所示,沿x轴正方向传播的一列简谐横波在某时刻的波形图为一正弦曲线,其波速为200m/s,下列说法正确的是( )
如图所示,沿x轴正方向传播的一列简谐横波在某时刻的波形图为一正弦曲线,其波速为200m/s,下列说法正确的是( )
 如图所示,沿x轴正方向传播的一列简谐横波在某时刻的波形图为一正弦曲线,其波速为200m/s,下列说法正确的是( )
如图所示,沿x轴正方向传播的一列简谐横波在某时刻的波形图为一正弦曲线,其波速为200m/s,下列说法正确的是( )| A. | 图示时刻质点b的加速度正在增大 | |
| B. | 从图示时刻开始,经过0.01 s,质点b通过的路程一定为0.4 m | |
| C. | 若此波遇到另一列简谐横波并发生稳定干涉现象,则该波所遇到的波的频率为50 Hz | |
| D. | 若该波发生明显的衍射现象,则该波所遇到的障碍物尺寸一定比4 m大 |
10.下列说法中正确的是( )
| A. | 任何带电体所带的电荷量都是元电荷e的整数倍 | |
| B. | 在真空中,电场强度的表达式 E=$\frac{kQ}{{r}^{2}}$中的E与Q无关 | |
| C. | 由 E=$\frac{F}{q}$可知此场中某点的电场强度E与F成正比 | |
| D. | A、B两点间的电势差等于将正电荷从A移到B点时静电力所做的功 |
7.太阳与地球的距离为1.5×1011m,地球的公转周期为1年.假设太阳系等比例缩小.即天体的直径和间距同比例变小;且各天体的平均密度不变.当太阳与地球的距离减小为0.75×1011m时,地球的公转周期为( )
| A. | 2年 | B. | 1年 | C. | $\frac{\sqrt{2}}{2}$年 | D. | $\frac{\sqrt{2}}{4}$年 |
8.关于物体的运动,下列说法正确的是( )
| A. | 物体运动的路程可能为0 | |
| B. | 物体位移的大小不可能大于路程 | |
| C. | 物体位移的大小一定小于路程 | |
| D. | 两运动 物体相比较,位移大则路程一定大 |
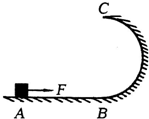 如图所示,平直轨道与竖直半圆形轨道平滑连接,圆形轨道半径R=2.0m,所有轨道均光滑.在A点开始用一水平力F=10N拉动质量m=1.0kg的物块(可视为质点),经1s向右移动5m到达圆形轨道的最低点B,撤去拉力.g取10m/s2,求:
如图所示,平直轨道与竖直半圆形轨道平滑连接,圆形轨道半径R=2.0m,所有轨道均光滑.在A点开始用一水平力F=10N拉动质量m=1.0kg的物块(可视为质点),经1s向右移动5m到达圆形轨道的最低点B,撤去拉力.g取10m/s2,求: