题目内容
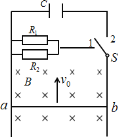
【题目】如图所示,两根足够长的平行竖直导轨,间距为 L,上端接有两个电阻和一个耐压值足够大的电容器, R1∶R2 2∶3,电容器的电容为C且开始不带电。质量为m、电阻不计的导体棒 ab 垂直跨在导轨上,S 为单刀双掷开关。整个空间存在垂直导轨平面向里的匀强磁场,磁感应强度大小为 B。现将开关 S 接 1,ab 以初速度 v0 竖直向上运动,当ab向上运动 h 时到达最大高度,此时迅速将开关S接 2,导体棒开始向下运动,整个过程中导体棒与导轨接触良好,空气阻力不计,重力加速度大小为 g。试问:
(1) 此过程中电阻 R1产生的焦耳热;
(2) ab 回到出发点的速度大小;
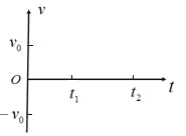
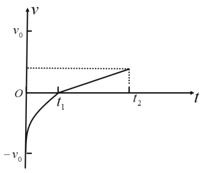
(3)当 ab以速度 v0向上运动时开始计时,t1时刻 ab到达最大高度 h 处, t2时刻回到出发点,请大致画出 ab从开始运动到回到出发点的 v-t 图像(取竖直向下方向为正方向)。
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析。
;(3)见解析。
【解析】
(1)只有当开关S接1时回路中才有焦耳热产生,在导体棒上升过程,设回路中产生的焦耳热为Q,根据能量守恒有
![]()
又![]() ,因此电阻R1产生的热量为
,因此电阻R1产生的热量为
![]()
![]()
(2)当开关S接2时,导体棒由静止开始下落,设导体棒下落的加速度为a,由牛顿第二定律得
mg-ILB=0
又
![]()
联立得
![]()
所以导体棒做初速度为0,加速度为a的匀加速直线运动,设导体棒回到出发点的速度大小为v,由![]() 得
得
![]()
(3)当导体棒向上运动时,由于所受安培力向下且不断减小,所以导体棒做加速度逐渐减小的减速运动;当导体棒开始向下运动时做初速度为0的匀加速直线运动,由于所受安培力与重力反向,所以此过程加速度小于g.

练习册系列答案
相关题目