Question

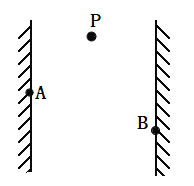
【题目】如图所示，质量相等的甲、乙两小球以大小相等的初速度分别自两竖直墙中的某点P水平向左、向右抛出。甲球抛出后击中左墙的A点，速度方向与竖直墙面夹角为α；乙球抛出后击中右墙的B点，速度方向与竖直墙面夹角为β。已知A点高于B点，则下列说法中正确的是（　　）

A.P点在两墙水平连线的中点

B.两球在空中的运动时间相等

C.甲球击中A值的速度大于乙球击中B点的速度

D.击中墙时，两角度一定满足关系α>β

Answer 1

【答案】D

【解析】

AB．小球做平抛运动，分解位移

根据题意可知

所以

所以乙球下落时间更长，点不是两墙水平连线的中点，AB错误；

C．两球水平速度相同，竖直方向做自由落体，根据

可知乙球竖直方向速度更大，根据速度合成可知乙球击中点的速度更大，C错误；

D．平抛运动分解末速度

乙球竖直方向速度大，则正切值小，所以击中墙时，两角度一定满足关系

D正确。

故选D。