题目内容
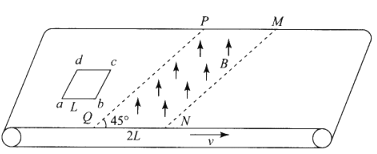
【题目】如图甲所示，在直角坐标系xOy中的四个点P（O，L）、Q（L，0）、M（0，-L）、N（-L、0）为PQMN的四个顶点，在△PQN范围内分布着匀强磁场，磁感应强度B随时间变化的图像如图乙所示（图像中T为未知量），设垂直纸面向外为正方向；△MQN内的匀强磁场与△PQN内的磁场总是大小相等、方向相反。在PQMN区域外，分别存在着场强大小为E的匀强电场，其方向分别与正方形区域PQMN在各象限内的边界垂直且指向正方形内部。质量为m、电荷量为q带正电的粒子在0
内某一时刻从原点O沿y轴正方向射入磁场，此后在xOy平面内做周期性运动。已知粒子在电场内做直线运动，且每当磁场方向发生变化时粒子恰好从电场射磁场。重力不计，忽略粒子运动对电、磁场的影响。上述L、B0、m、q、E为已知量。
(1)若粒子从出发到第一次回到O点过程中，在磁场中运动的时间小于
，求该粒子的初速度；
(2)求满足第一问条件下，粒子从出发到第一次回到O点的路程；
(3)求粒子初速度的所有可能值及对应的磁场变化的周期T。
【答案】(1)
；(2)
；(3) 
（n=0，1，2，3，…），
（n=0，1，2，3，…）
【解析】
(1)若粒子从出发到第一次回到O点过程中，在磁场中运动的时间小于
，则粒子在磁场中的轨迹如图1所示
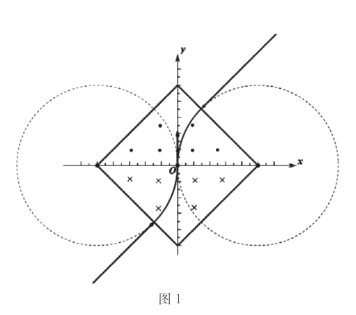
由几何关系得
粒子在磁场中运动时，洛伦兹力提供向心力，则
解得粒子的初速度
(2)满足第一问条件下，设粒子在电场中轨迹的长度为x1，则
解得粒子在电场中轨迹的长度
粒子从出发到第一次回到O点的路程
(3)粒子在xOy平面内的周期性运动，一周期内，粒子在磁场中运动时间可能为
，其中n=0，1，2，3…...。当n=0，1，2时，轨迹分别如图1、2、3所示
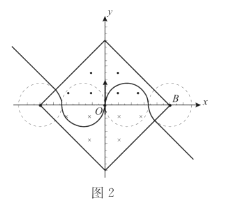
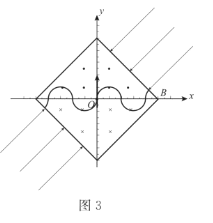
由以上分析可知，粒子在磁场中做圆周运动的半径的可能值为
根据洛伦兹力提供向心力，则有
可得初速度的所有可能值为
一个周期内粒子在电场中运动的可能时间为
磁场变化的周期T的可能值为
其中n=0，1，2，3，…
