Question

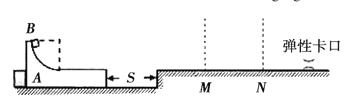
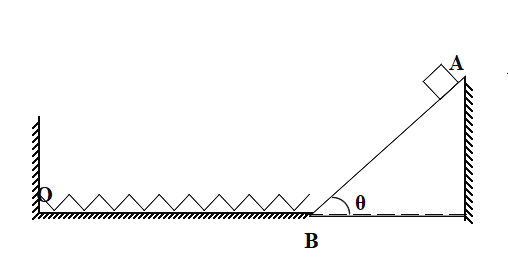
【题目】如图所示，小滑块（视为质点）的质量m= 1kg；固定在地面上的斜面AB的倾角=37°、长s=1m，点A和斜面最低点B之间铺了一层均质特殊材料，其与滑块间的动摩擦因数μ可在0≤μ≤1.5之间调节。点B与水平光滑地面平滑相连，地面上有一根自然状态下的轻弹簧一端固定在O点另一端恰好在B点。认为滑块通过点B前、后速度大小不变；最大静摩擦力等于滑动摩擦力。取g=10m/s2 ，sin37° =0.6，cos37° =0.8，不计空气阻力。

（1）若设置μ=0，将滑块从A点由静止释放，求滑块从点A运动到点B所用的时间。

（2）若滑块在A点以v0=lm/s的初速度沿斜面下滑，最终停止于B点，求μ的取值范围。

Answer 1

【答案】（1）s；（2）或。

【解析】

（1）设滑块从点运动到点的过程中，加速度大小为，运动时间为，则由牛顿第二定律和运动学公式得

解得s

（2）滑块最终停在点，有两种可能：

①滑块恰好能从下滑到，设动摩擦因数为，由动能定律得：

解得

②滑块在斜面和水平地面间多次反复运动，最终停止于点，当滑块恰好能返回点，由动能定理得

解得

此后，滑块沿斜面下滑，在光滑水平地面和斜面之间多次反复运动，最终停止于点。

当滑块恰好能静止在斜面上，则有

解得

所以，当，即时，滑块在斜面和水平地面间多次反复运动，最终停止于点。

综上所述，的取值范围是或。